余りの求め方≫ それでは,最初の問題を解いて,具体的に余りの求め方を考えてみましょう。 問題1の解答 剰余の定理より,整式 x100 1に x =1を代入して, 1 100 1=11=2 よって, x100 1 を x 1で割った余りは, 2 ・・・・・・ (答) 問題2の解答 この問題
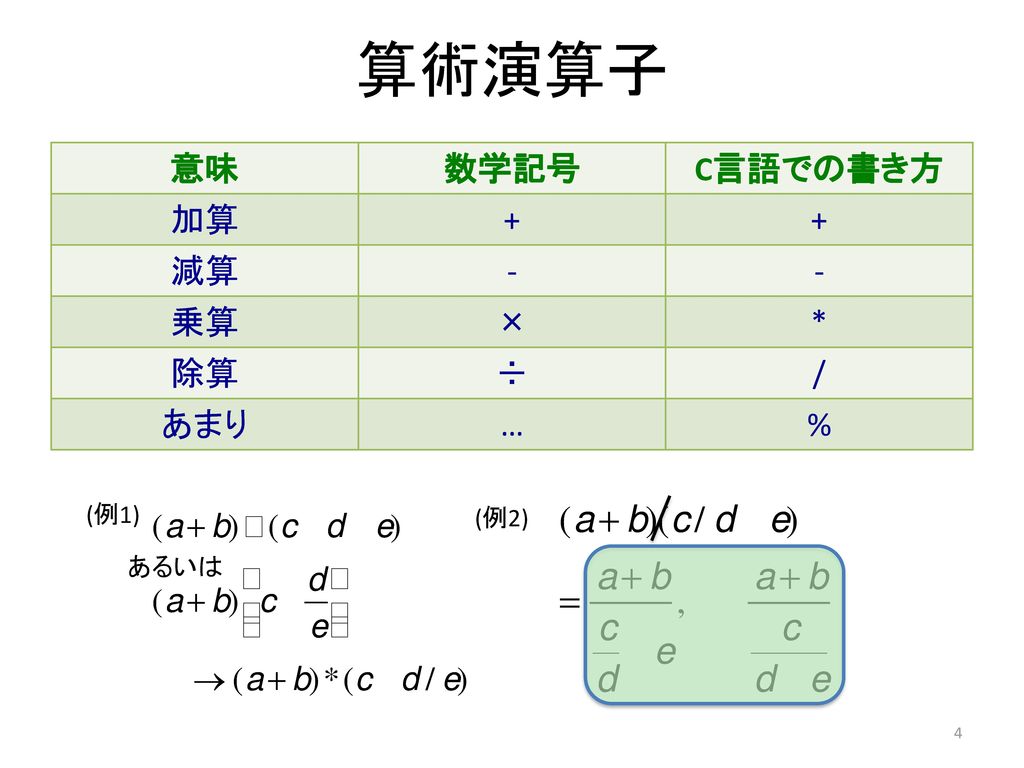
余り 記号-記号 名称 / 読み方 Unicode 文字参照 実体参照 L a T e Xコマンド ;割られる数が の場合、割る数と答えを掛け算することで答えを求めることができます。 もし余りがある場合は、余りを足し合わせます。 ÷2=3 → =2×3 → =6 ÷3=2•••1 → =3×21 → =7 割る数が の場合、割われる数を答えで割り算することで答えを求める
余り 記号のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
 |  |  |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 | ||
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 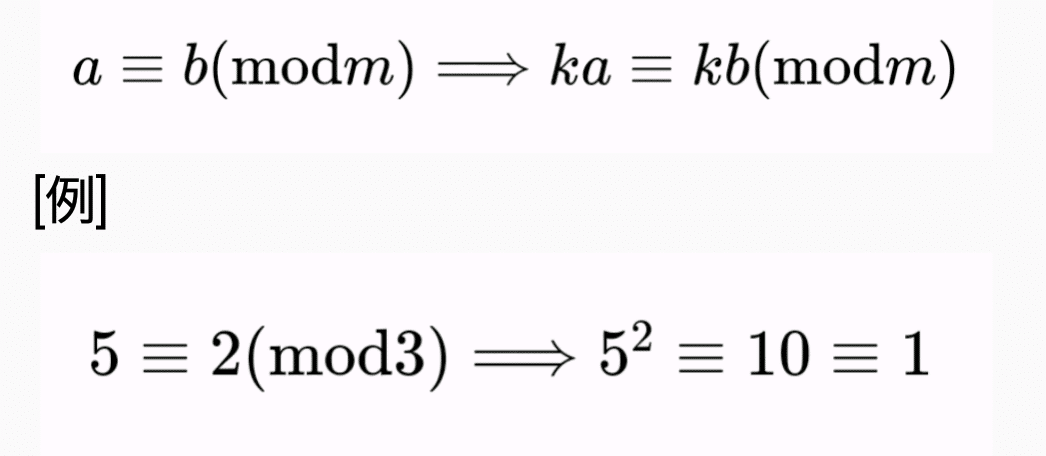 | |
 |  |  |
 |  | |
 |  | |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |
記号 意味 解説 剰余 「 x mod y 」は整数 x の属する法 y の剰余類や、 x を y で割った余りを表す 要出典 。C言語やその影響を受けたプログラミング言語などでは整数の剰余を与える演算子として % が定義されている 。分かりにくいよ、三角マーク 実例 企業の決算報告や会計関連の本を読んでいると、 マイナスを表すのに「 100,000」や「 100,000」といった上向きの三角形が使われていることがあります。 トヨタの決算報告書より。 白の三角形。 ソニーの決算報告書より
Incoming Term: 余り 記号,




0 件のコメント:
コメントを投稿