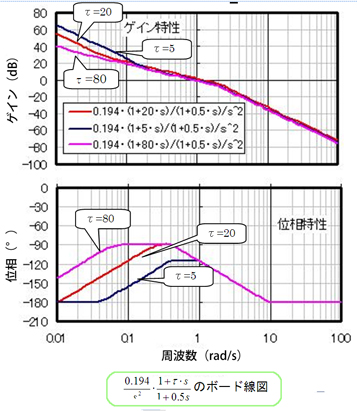
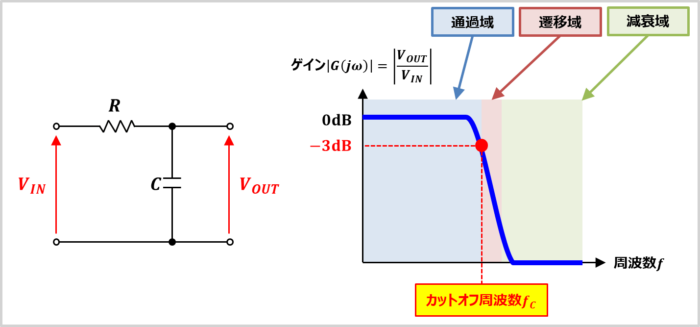
成立していない一例として、図21 の定数での21 式の最大ゲインは約105 倍、その時の正規化周波数 は約075 と計算されるが、実際の最大伝達比T(peak)とその周波数fp は次の様になる。 608KHz (06 ) ( ) ( ) Vin 0300Vp fr 100KHz 倍 倍 条件: fp Vin Vout T peak 1 23 150 185カットオフ周波数(遮断周波数) Cutoff Frequency 遮断周波数とは、右図における信号の通過域と遷移域との境界となる周波数である(理想フィルタでは遷移域が存在しないので、通過域と減衰域との境が遮断周波数である)。 通過域から遷移域へは連続的に周波数 に対し 5 周波数応答 53 ボード線図 の変化を表すゲイン曲線 の変化を表す位相曲線 横軸:周波数 を対数目盛り 縦軸:ゲイン曲線 デシベル値(dB) 位相曲線 度 絶対値 デシベル値 1 デ
ボード線図
折れ点周波数 求め方
折れ点周波数 求め方-Break frequency 機械力学・計測制御 ボード線図のゲイン線図を何本かの漸近線で近似することがある.この近似を折線近似と呼び,この折れ曲がる点を折点,折点に対応する周波数を折点周波数とい周波数リミッタ、周波数ジャン プ、曲線加減速、手動トルク ブーストレベル・折れ点、省エ ネ運転、アナログメータ調整、 始動周波数、キャリア周波数 調整、電子サーマル機能、(自由 設定も可)、外部スタート・エンド (周波数・割合)、アナログ入力



制御工学 一次遅れ要素のボード線図で 折れ点角周波数がなぜ決まるか Yahoo 知恵袋
返し数でもなだらかに下がり続けている黄銅やアルミ合 金などの非鉄金属では,明確な折れ点が現れず炭素鋼のよ うな疲労限度を定義することができないこのような場合 には,sn曲線上で特定の繰返し数(例えば1x 107回)•低周波領域ωω/ωn) • 0dBの水平線 •交点(折点周波数) •ω/ωn=1→固有角周波数ω=ωn •減衰比ζで共振点でのピーク値が変わる • 折れ線での近似値0dB • 減衰比ζが小さいと,ピークが大きくなり,近似からの乖離大 log 1 2 log1 0dB 2 2 2 2機械工学演習C課題10 (周波数応答2) 66 周波数伝達関数が次式で示される1次遅れ要素の折れ点周波数を求めよ.また,その点でのゲイ ンをデシベルで示せ. (1) G jω 7 1 j0 02ω (2) G jω 1 j40ω 67 図101 はある自動制御系の周波数伝達関数をボード線図上で折れ点
周波数応答は,入力の角周波数ωに対するゲインP(jω) と位相 P(jω) で与えることができ ます。 これらを図に描く場合,いくつかの組み合わせが考えられます。周波数伝達関数の場合も logP(jω)K(jω)=logP(jω)logK(jω) 足し算を図で考えたいがlogP(jω)K(jω) は複素数 例:P(s)K(s)= 1 s 1 ⇒P(jω)K(jω)= 1 jω1 まずは一般の複素数Z に対してlogZ の図示を考える 実部,虚部に分けてみる 浅井 徹 (名古屋大学) ボード線図のしくみ•折れ点周波数=直線の傾きが変わる周波数 微積分要素 便宜的 1次要素 分子:+,分母: dB/dec 2次要素 分子:+40,分母:40 dB/dec 0 rad/s ω nrad/s 1/Trad/s 1次要素の折れ点周波数
JPB2 JPA JPA JPB2 JP B2 JP B2 JP B2 JP A JP A JP A JP A JP A JP A JP B2 JP B2 JP B2 Authority JP Japan Prior art keywords vehicle driver frequency panel automobile Prior art date Legal status (The legal status is an=!0 の適当な 正弦波を加えると,出力も角周波数!0 の正弦波となる.このとき,入力x(t) と出力 y(t) のラプラス変換をそれぞれX(s);折れ点の周波数がカットオフ周波数です。 PI 動作や PD 動作では、積分時間 TI、微分時間 TDが、1 次遅れの時定数 TL と同じ意味を持っています。 ★ 複数の制御要素をカスケード接続したとき、全体の特性は、 ボード線図 上では加算になります( コラム 322 )。



Eee Kagoshima U Ac Jp



Kspub Co Jp
上記の周波数伝達関数のボード線図を図6‑7に示す.図から明らかな通り,ゲイン特性は dB/decade,位相特性は 90 deg (90度の位相進み) となる.上記から明らかな通り,微分要素は角周波数が高い領域でゲインが高くなるため,ノイズの影響を非常に受けやすい問題点がある.また,角周波数This document you requested has moved permanently It's now at /help/control/ref/ltimarginhtml;jsessionid=1a0d0deb2f6afcebbfc85• 折点周波数を中心に奇対称(atan) • 直流0° • 折点周波数45° • ∞→90° 1jωT 1 φ=−tan−1ωT =−tan− =−tan−1 1=−45o T T ω ω φ




正弦波振動試験 加速度 振幅 周波数に関する計算式 Show Notes



ボード線図
フィードバック制御系の設計 前章までに学んだことを踏まえ, – 安定性,減衰性,速応性,定常特性を用いて, 制御系の設計仕様を定量的に表現できる – 補償要素を加えることによって,設計仕様を 満たす制御系を設計できる • 直列補償位相遅れにより安定性が劣化しないように 折点角周波数 をゲイン交差周波数より dec 程度下になるように 選ぶ。もうひとつの折点角周波数を と定める。 ステップ1の を用いて開ループ伝達関数のボード 線図を描き, その低周波ゲインを評価する。「制御工学」第9回(補足) ボード線図のゲイン特性の描き方 ボード線図のゲイン特性の描き方 実際の制御系の周波数応答とゲイン () ゲイン特性(分子)の折れ線近似 各要素のゲイン特性(分子) ゲイン特性(分母)の折れ線近似 ボード線図の折れ線近似(まとめ) 鹿児島大学



折れ 点 角 周波数




ボード線図を書こう Keio Robotics Association
論文 dcサ ーボモータの動特性に関する考察* -サーボ増幅器内の回路定数の推定- 酒井史敏**神 谷好承***関 啓明***疋 津正利*** 周波数伝達関数は、伝達関数の複素数 $s$ の関数の代わりに $jω$ で表します。 周波数伝達関数を $G(jω)$、入力を $X(jω)$、出力を $Y(jω)$ としたとき、$G(jω)=\displaystyle\frac{Y(jω)}{X(jω)}$ と定義されます。 ブロック線図の等価変換の計算The total length of a going path from the feed point 21 of the first antenna element to a return point and a return path from the return point to the feed point 21 corresponds to a half of the wavelength at first resonance frequency 特許庁 同様に、使用上限 周波数 f_2の第2加速度センサ12を直接固定し、同特性の第2加速度センサ12を 折 れ 点周波数



Asahi Net Or Jp



これで完全マスター Pid制御 独学 機械設計者のための自動制御入門 10 3 3 ページ Monoist
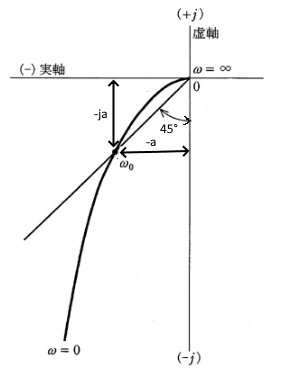
電圧、周波数(同時急変可能) 折れ点数 1~100 スイープ開始位相 設定範囲 0°~359° (位相分解能 1°) 遷移時間 設定範囲 0(50μs)~ms(各折れ点間) (設定分解能:1ms) 設定確度 設定値の±01%±2ms 繰り返し回数 設定範囲周波数 0°45° w0 0 log w ww0 : 折点周波数 ボード線図による安定性判別 s平面の虚軸に対応するナイキ スト軌跡R(jw) は一巡伝達関 数の周波数応答を表す ナイキスト軌跡が点(1,0)の下 を潜れば安定 一巡伝達関数のボード線図でゲ インが0dBのときに位相遅れが直線的に補正されるドループ補正周波数に折れ点を設け、より適切な補正が可能となります。 パラメータ番号 名称 初期値 設定範囲 994 ドループ折れ点ゲイン 9999 01~100%,9999 995 ドループ折れ点トルク 100% 01~100%




Rcローパスフィルタとrlハイパスフィルタの勉強 その1 Sora S Activity Record
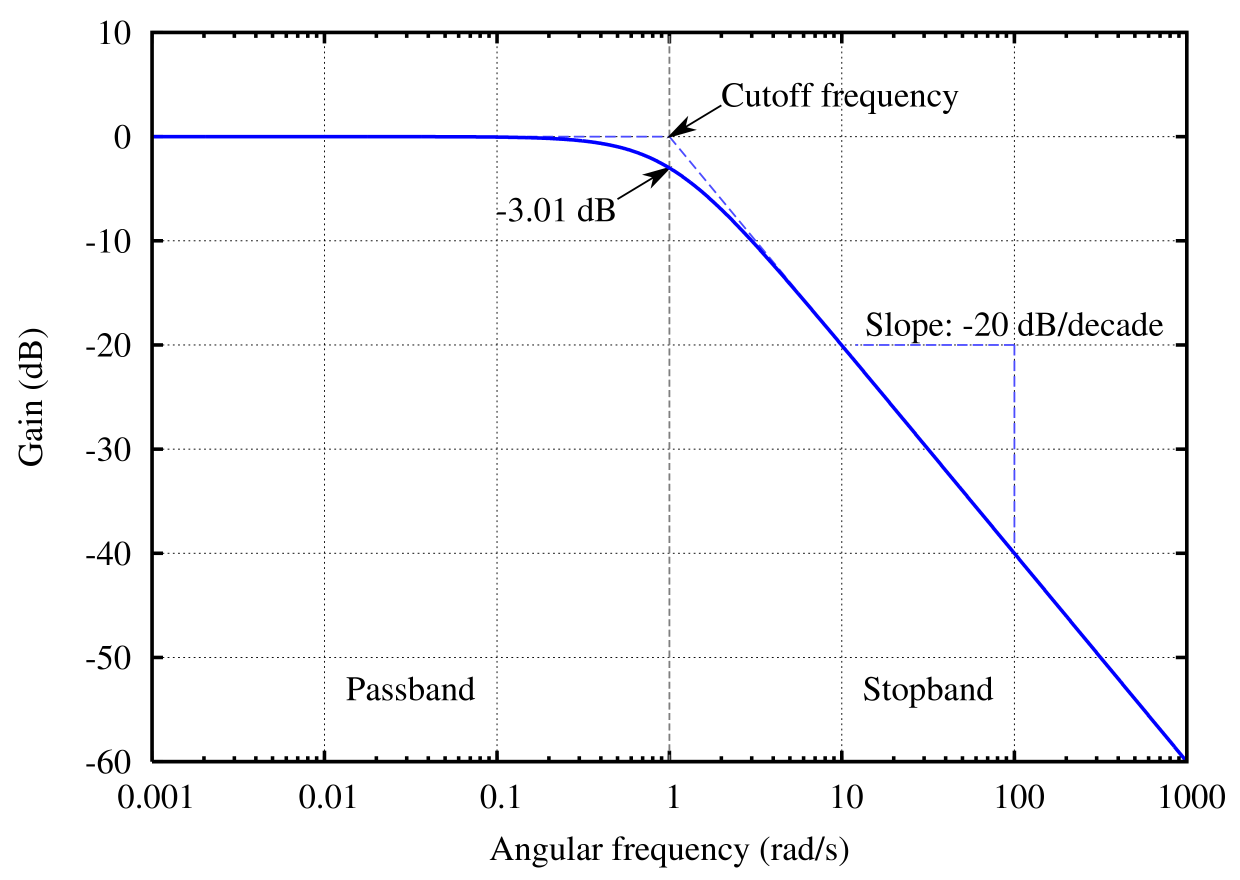



遮断周波数 Wikipedia
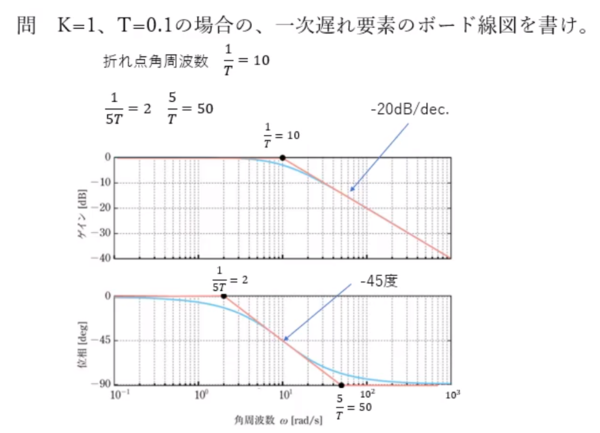
ゲイン線図が曲がりはじめるところ、位相が\(45deg\)を通過するところの角周波数を 折れ点周波数 と呼びます 折れ点周波数は時定数の逆数\(\frac{1}{T}\)になります 上の例だと折れ点周波数は\(10^{0}\)と、時定数の逆数になっています¨ ゲイン特性は, w = 1/T まで 0dB で,その点からdB/dec の傾きで下がる折れ線に近似できる. w = 1/T を 折れ点周波数 と呼ぶ. 現在のシステムでは, bode 関数は非プロパーな伝達関数も扱うことができるが, M ファイルの作成方法を学習するため, bode1m を作成する.Contribute to griffin921/BuckConverter development by creating an account on GitHub



ボード線図を書こう Keio Robotics Association



制御工学 一次遅れ要素のボード線図で 折れ点角周波数がなぜ決まるか Yahoo 知恵袋
ゲイン: (折点周波数)の周波数で の直線 の周波数で の直線 の周波数の点は を通る。 位 相: の周波数(折点周波数)で の線 (近似的に) の周波数で の線 の周波数で の線周波数伝達関数は,角周波数ωの複素関数である. 従って,その表現法には,2方式がある ベクトル軌跡(vector locus / polar plot): 実数部と虚数部をもつ2次元ベクトルの終端がωの変化に対して複素平面上を動く奇跡とPr994、Pr995 を設定することで、ドループ補正周波数に折れ点(1点)を設けることができま す。これにより、重負荷時のドループ補正周波数は上げずに、軽負荷時(無負荷時)のドループ 補正周波数を上げられるようになります。



Sma Jaxa Jp



機械 制御 H27 問17 フィードバック制御の伝達関数に関する計算問題 電験王3
RC方式の積分回路の設計手順&設計ポイントを紹介 基本的な設計手順は以下となります。 通過させたい信号の周波数を確認する カットしたい信号の周波数を確認する 設定するRとCの定数を決定する(時定数を決める) シュミレーションを又は回路を組んY(s) とおくと,次の関係が成り立つ. G(s) = Y(s) X(s) (伝達関数の定義)折点周波数を英語で訳すと corner frequency 約1174万語ある英和辞典・和英辞典。発音・イディオムも分かる英語辞書。
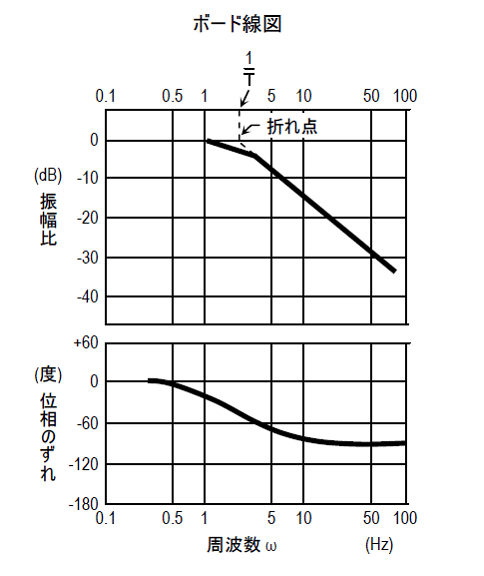



用語集 新川電機株式会社 計測 制御のスペシャリスト




Speedy Character Line Detection Algorithm Using Image Block Based Histogram Analysis Springerlink
(57)要約 目的ばね下の共振周波数を越える振動に対して減衰 力が過大になることを防止して、車体および乗員への振 動の伝達を遮断する。 構成伸びる時、上作動室30の体積は減少し、下作 動室33の体積は増加するため、下作動室33内の作動 油が穴45、油路18、制御弁9、油路また、 ωは角速度(または角周波数ともいう)と呼ばれ、周波数 fとは ω=2π×fの関係式で表されます。 たとえば下式(1) のように、伝達関数 sY/(1sX)に s=jωを代入すると jωY/(1jωX)を得ます。 ・・・ (1) つまり、任意の周波数 f(f=ω/2π)のサイン波に対する挙動を上式は表しています。 虚数 jを使ってなぜサイン波に対する挙動を表すことができるかについては角周波数 $$\omega=1/T$$ を 折点周波数 おれてんしゅうはすう という。 図からわかるように、実際のゲイン曲線は、折点の $$3〔\mathrm{dB}〕$$ 下を通ることになる。




10 号 サーボ制御装置 Astamuse



第11回



H27 機械 解説17 Yaku Tik 電験三種まとめました
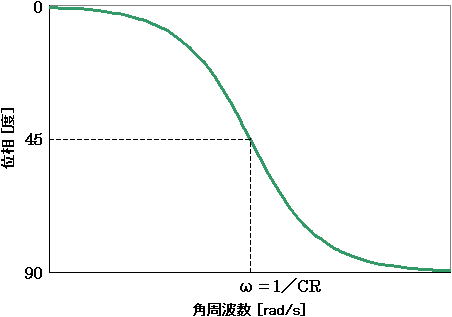



周波数特性とボード線図 わかりやすい 入門サイト



制御工学の質問です 一次遅れ系の折点周波数が時定数の逆 Yahoo 知恵袋



Scilab フィードバック制御入門 周波数応答 比例 微分 積分



Jaxa Repo Nii Ac Jp
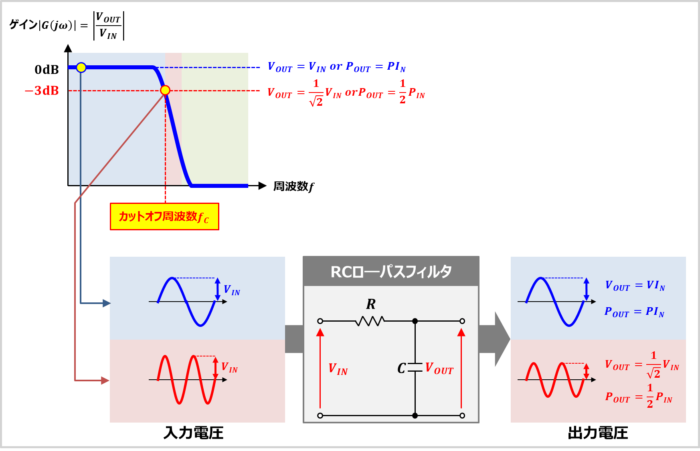



カットオフ周波数 遮断周波数 とは フィルタ回路 Electrical Information



三菱電機 ファンインバータ 型式 Fr Fs2 0 8k 材料 部品 ヤフー店 Diy 工具 送風機用単相インバータ 送風機用単相インバータ 配管部品



Ishikawa Nct Ac Jp
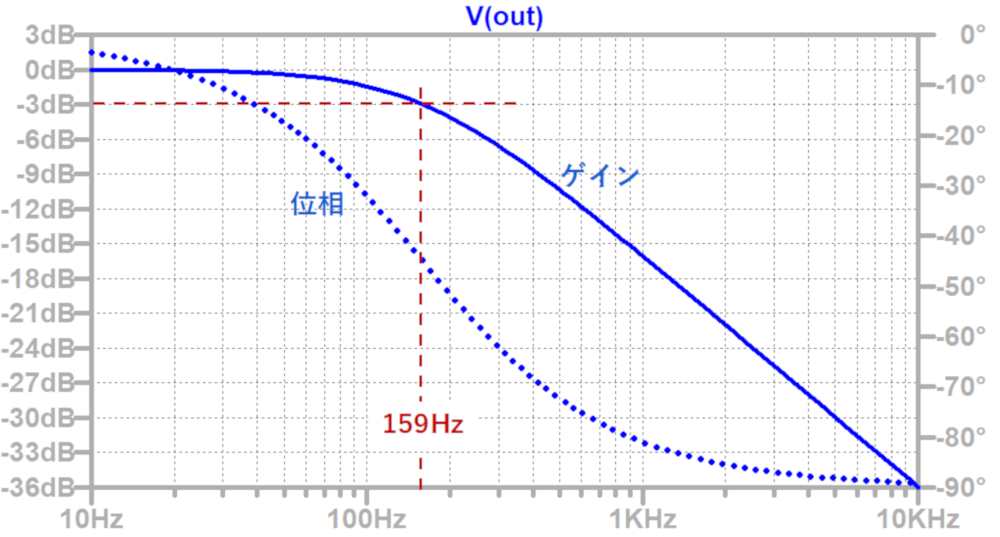



カットオフ周波数の求め方 Analogista



第14回



Ishikawa Nct Ac Jp




Rcローパスフィルタとrlハイパスフィルタの勉強 その1 Sora S Activity Record
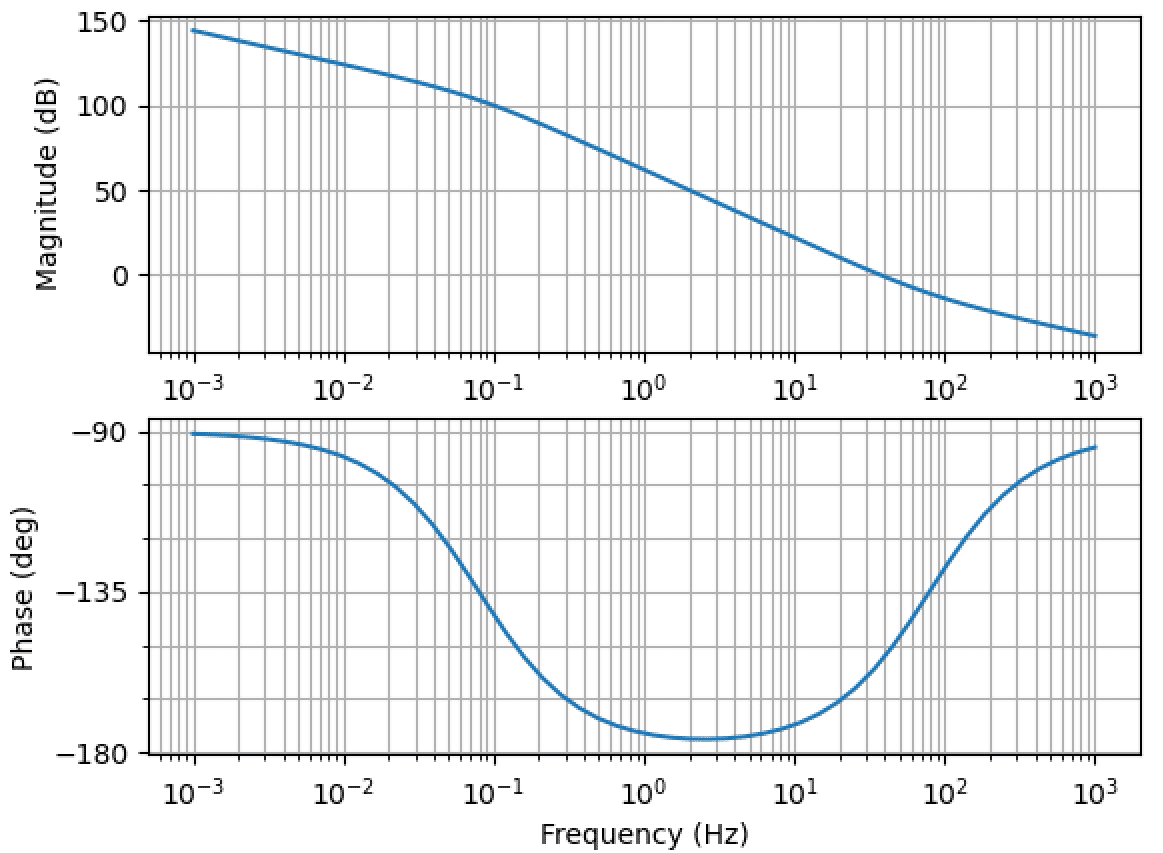



Python Control 電流フィードバック制御系の特性比較 Hiro Note




16 号 衝撃試験機および衝撃試験方法 Astamuse
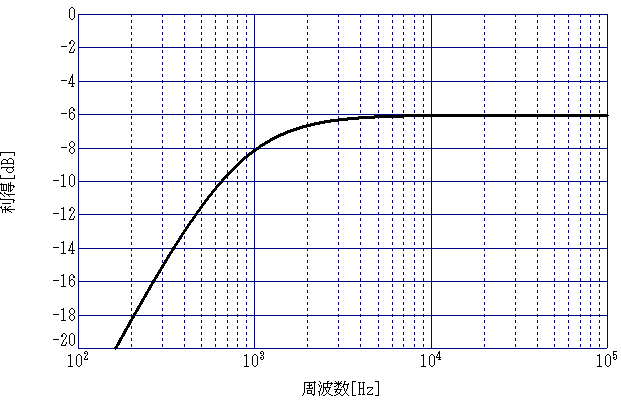



カットオフ周波数 の解説 しなぷすのハード製作記
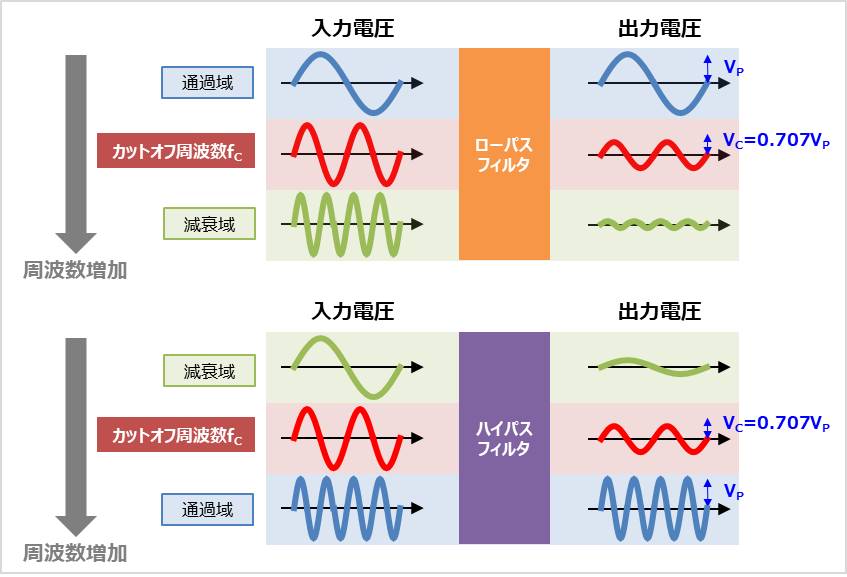



フィルタ回路 カットオフ周波数 遮断周波数 でゲインが 3dbになる理由 Electrical Information



制御工学 一次遅れ要素のボード線図で 折れ点角周波数がなぜ決まるか Yahoo 知恵袋



Repository Dl Itc U Tokyo Ac Jp



1




小野測器 Fft基本 Faq 時定数とローパスフィルタのカットオフ周波数の関係は



1



Ishikawa Nct Ac Jp



スイッチング回路
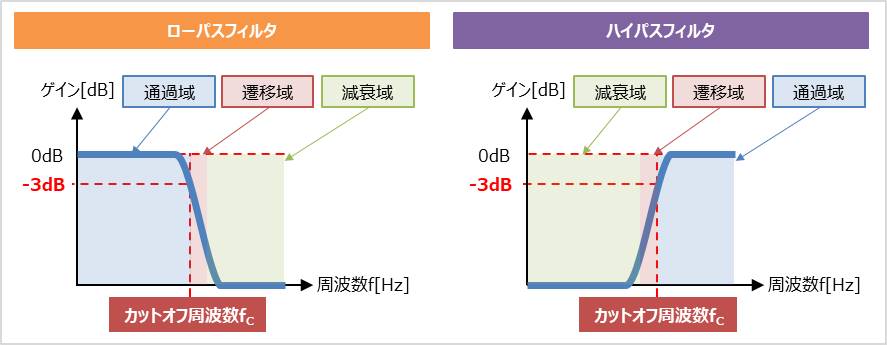



フィルタ回路 カットオフ周波数 遮断周波数 でゲインが 3dbになる理由 Electrical Information



Asahi Net Or Jp



カットオフ周波数 遮断周波数 とは フィルタ回路 Electrical Information



Kspub Co Jp



ブロック線図と伝達関数 基礎からわかる電気技術者の知識と資格



Nsr Go Jp




ボード線図を書こう Keio Robotics Association




ボード線図 ボーデ線図 とは E M Jobs



Fl Ctrl Titech Ac Jp




09 号 除振機構 Astamuse
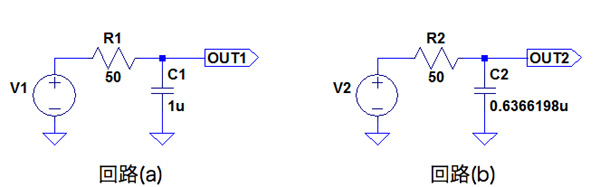



雑音が少ない1次ロー パス フィルタはどっち Cq出版社 オンライン サポート サイト Cq Connect
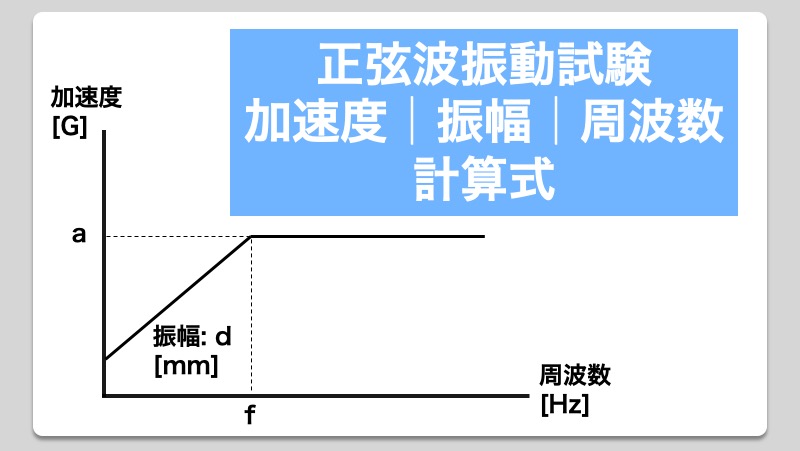



正弦波振動試験 加速度 振幅 周波数に関する計算式 Show Notes




19年度第07回電制研ゼミ開催 電力変換制御技術研究室 川上研究室



ボード線図




か 電験他 Forstudy7 Twitter




Wo15 号 電動パワーステアリング装置 Astamuse




1994 号 エレベータの電流制御系 Astamuse




21 号 撮像装置 振れ補正装置および振れ補正方法 Astamuse



制御工学5 ボード線図 画像処理プログラミング



電験三種 H27 機械 問17解説 電験三種 これでok




簡単なデジタルフィルタの実装 C でvst作り



制御の問題で ボード線図から伝達関数を求めたいのですが たとえば 一次遅れ系 Yahoo 知恵袋



伝達関数のボード線図のかきかたについて質問です g 10 1 S Yahoo 知恵袋



ボード線図の作図方法 折れ線近似 につきまして質問いたします 古典制御工 Yahoo 知恵袋



位相遅れ補償



Ishikawa Nct Ac Jp



H27 機械 解説17 Yaku Tik 電験三種まとめました




ボード線図を書こう Keio Robotics Association



ボード線図



3



カットオフ周波数 の解説 しなぷすのハード製作記



カットオフ周波数の求め方 Analogista



インバータ Freqrol A800シリーズ 三菱電機 株 Mitsubishi デジアナeカタログ メカトロネット



ボード線図の書き方 1次遅れ系




遮断周波数 Wikipedia



1
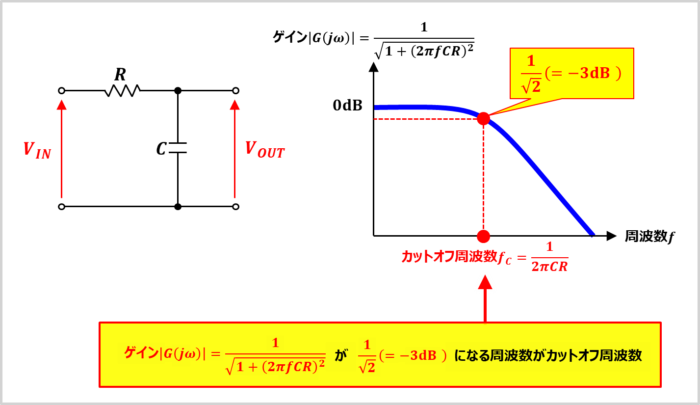



カットオフ周波数 遮断周波数 とは フィルタ回路 Electrical Information




1999 号 ケ ブル用等化器の直流減衰及び下側折点周波数の決定方法 ケ ブル用減衰等化器 減衰等化器 等化器各部品値決定方法 及びケ ブルアセンブリ Astamuse
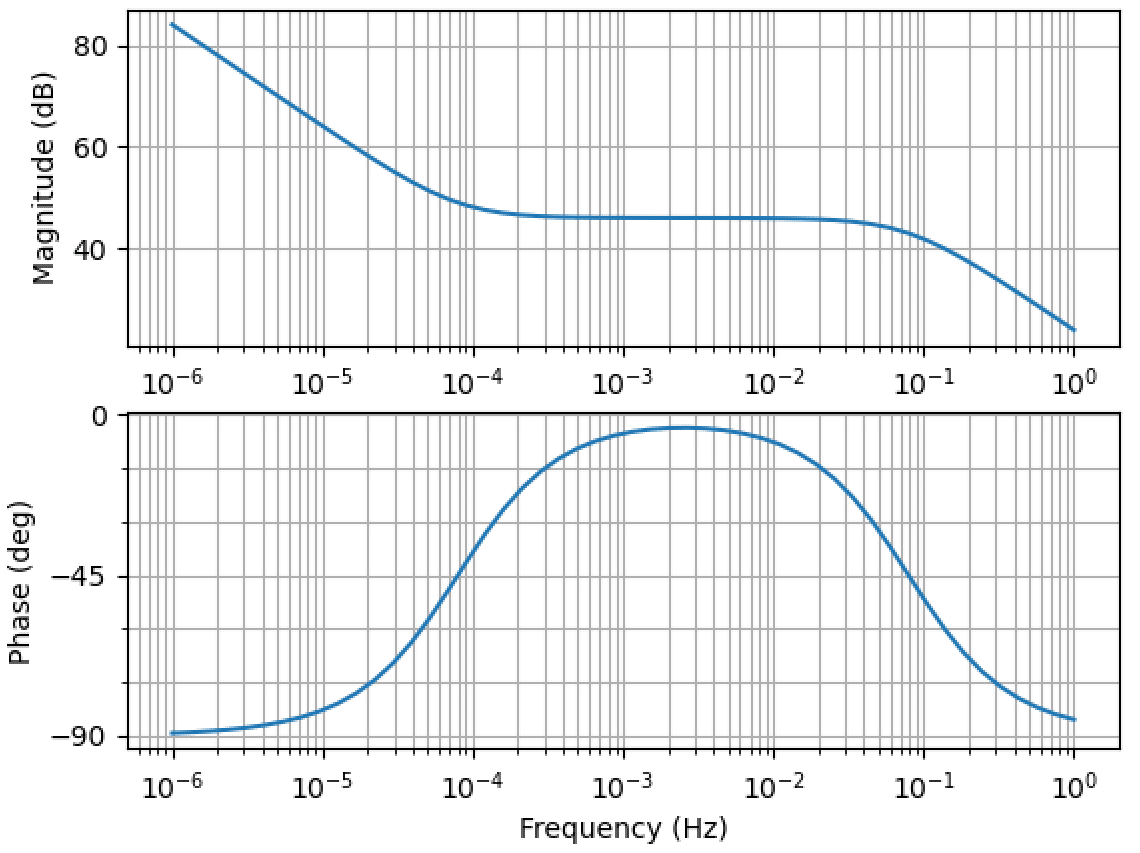



Python Control 電流フィードバック制御系の特性比較 Hiro Note
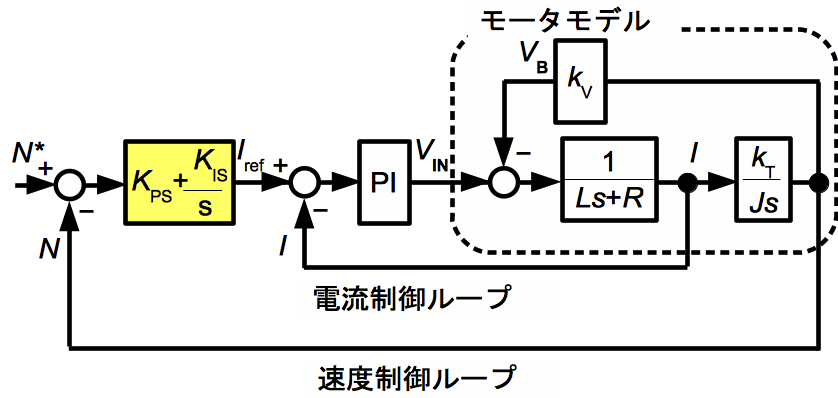



モータドライブ 制御系設計編
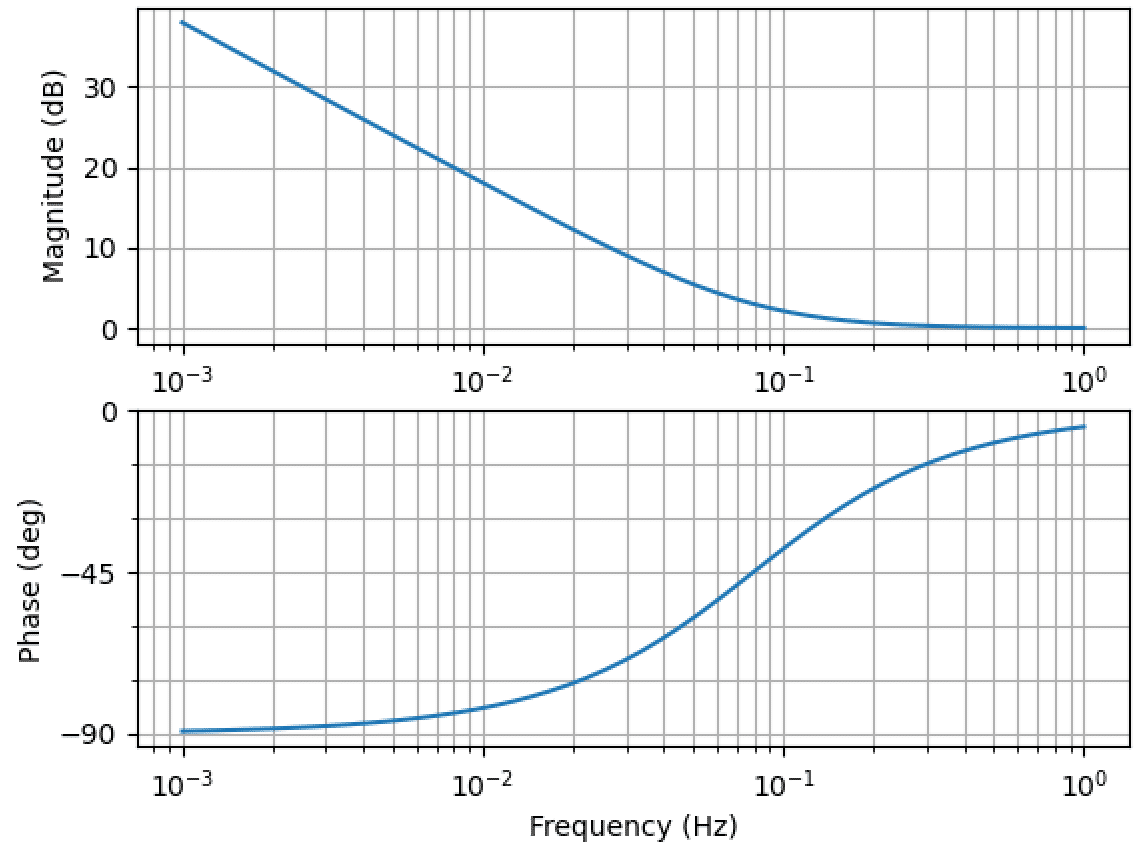



Python Control 電流フィードバック制御系の特性比較 Hiro Note



ボード線図
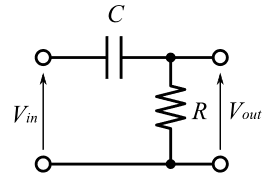



カットオフ周波数 の解説 しなぷすのハード製作記




みなみ ゆうき そういえば 位相線図の折点周波数を自分で求めたことがなかった気がする ちょっと計算すると 1次遅れ系1 1 Ts の場合 Omega T E Pi 2 0 2 と Omega T E Pi 2 5 になる ゲイン線図の方は Omega T 1 のところが折点



Jaxa Repo Nii Ac Jp



Scilab フィードバック制御入門 周波数応答 比例 微分 積分



H27 機械 解説17 Yaku Tik 電験三種まとめました
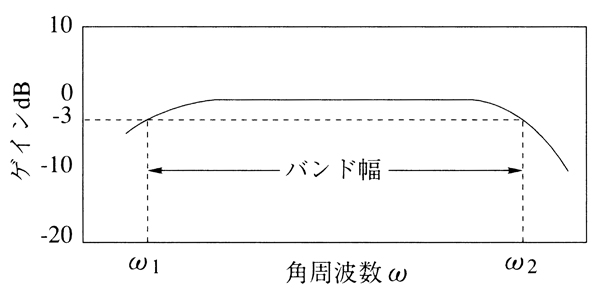



遮断周波数 Jsme Mechanical Engineering Dictionary




簡単なデジタルフィルタの実装 C でvst作り



Scilab フィードバック制御入門 周波数応答 比例 微分 積分
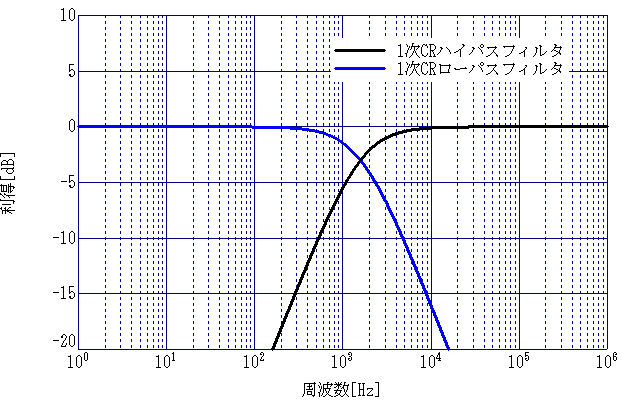



カットオフ周波数 の解説 しなぷすのハード製作記
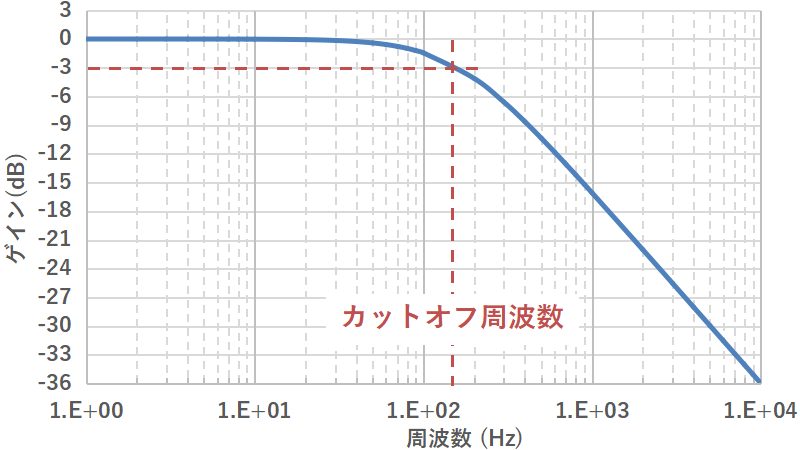



カットオフ周波数の求め方 Analogista
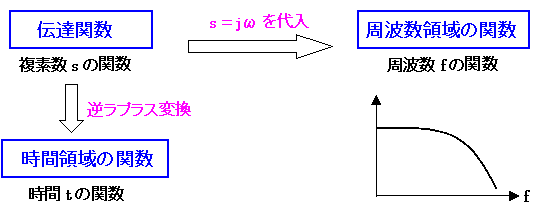



周波数特性とボード線図 わかりやすい 入門サイト




ブロック線図と伝達関数 基礎からわかる電気技術者の知識と資格



H27 機械 解説17 Yaku Tik 電験三種まとめました




13 号 衝撃試験機および衝撃試験方法 Astamuse



公開特許公報
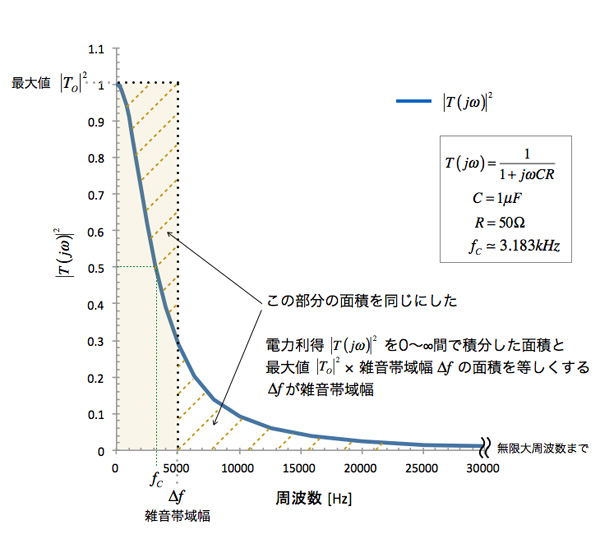



雑音が少ない1次ロー パス フィルタはどっち Cq出版社 オンライン サポート サイト Cq Connect




14 2365号 モータ制御装置 Astamuse



Asahi Net Or Jp



ボード線図
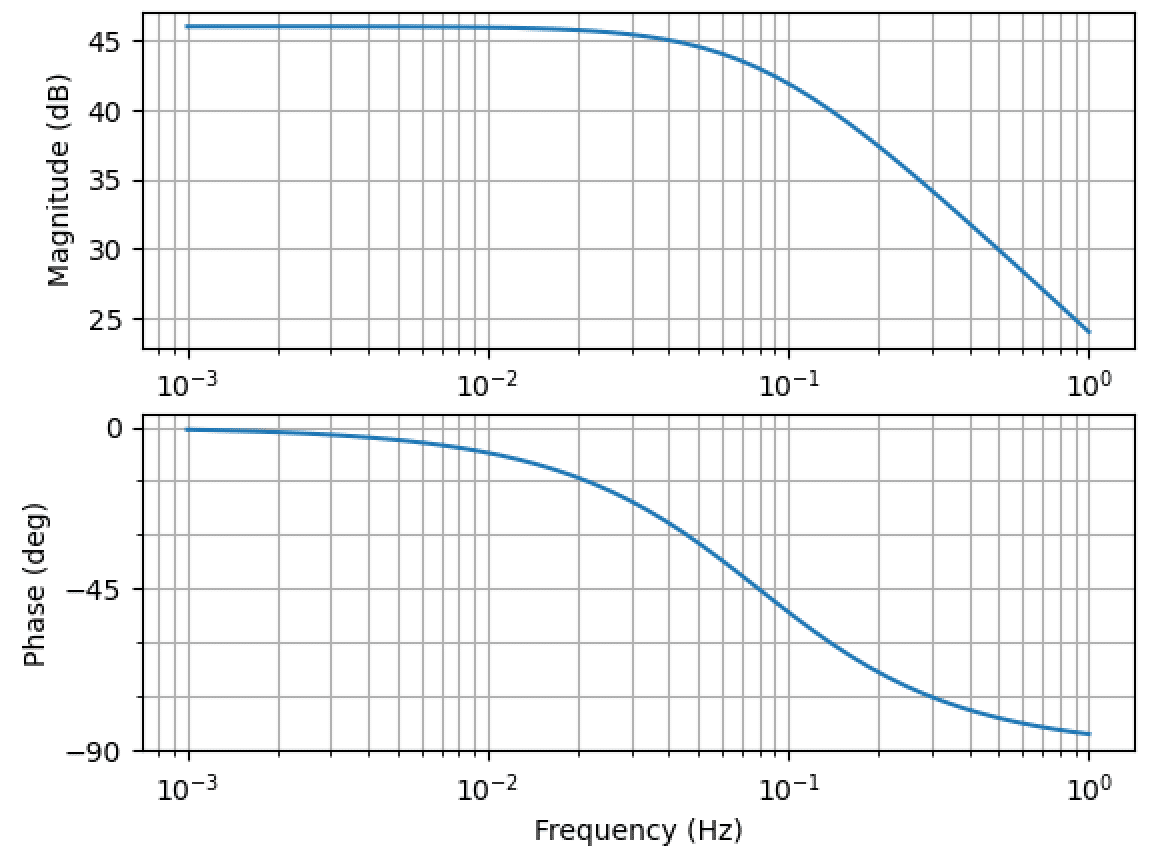



Python Control 電流フィードバック制御系の特性比較 Hiro Note




移動平均とローパスフィルタ ヤカンヒコウ



0 件のコメント:
コメントを投稿