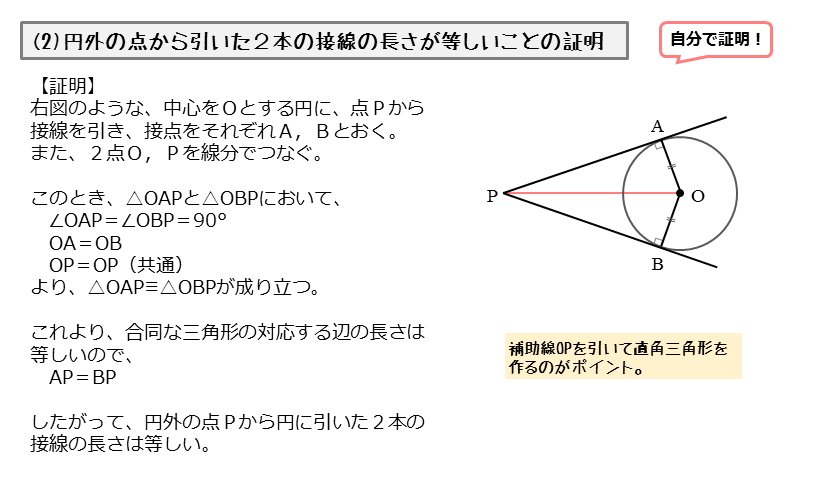
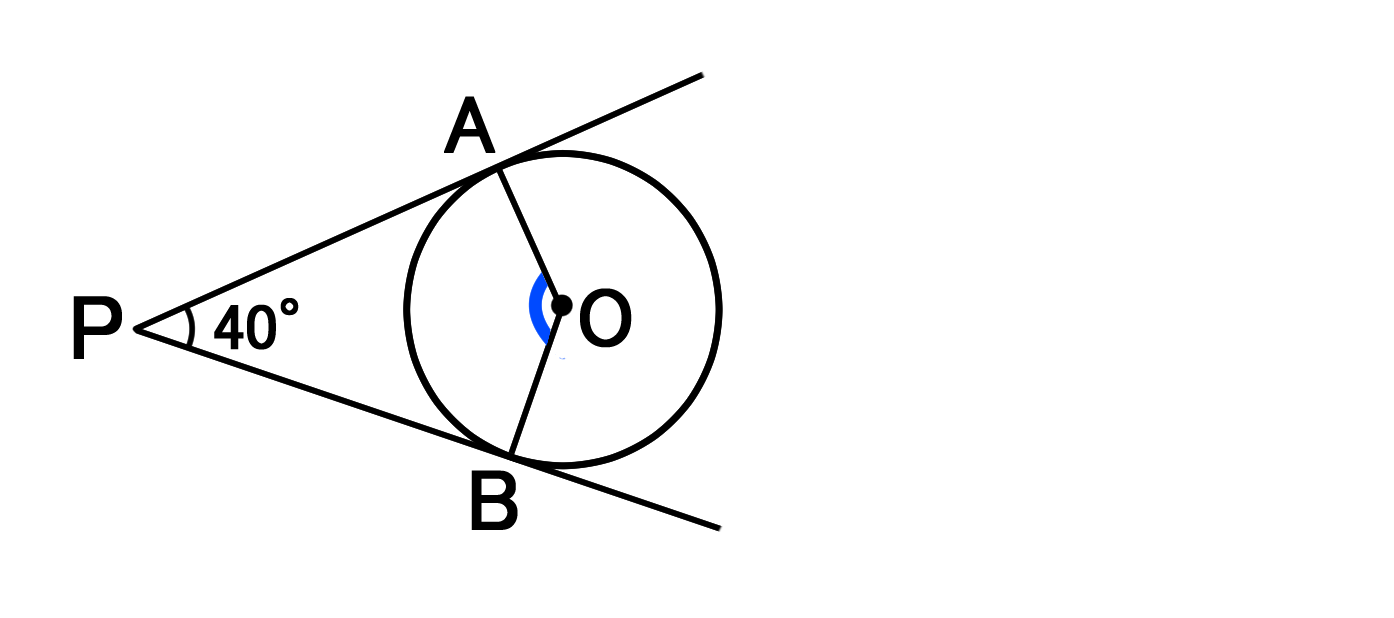
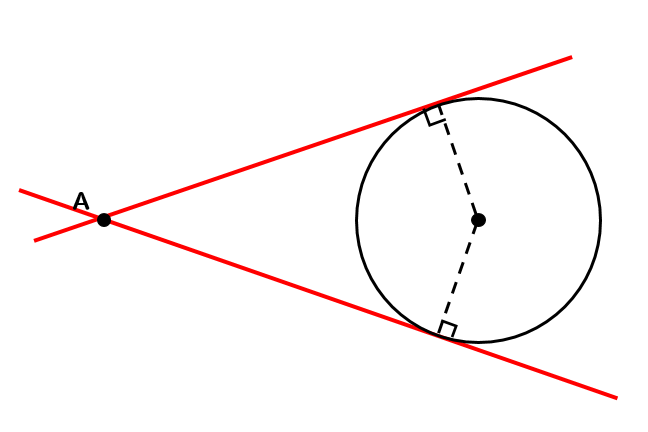
二つの円が交じり合うと、共通接線や弦ができます。 これを円同士が離れていても成り立つように拡張するにはどうしたらいいのでしょうか。 ジオジェブラの中にある極線を使うとできることに気がつきました。 この極線はとても大切な線です。5図形の性質と証明 円の接線を作図しよう 10 2 年 組 氏名 1 古代ギリシアの数学者ユークリッドは,いくつかの基本的な図形の性質をもとにして, 様々な図形の性質を証明し,有名な「原論」にまとめました。 この原論の第3巻に,「与えられた点から与えられた円に接線をひく」作図の方法が紹介図のように,円の外側の 1点P から円の接線を2本引いた時,点P と 接点A, B の長さは等しい。 (AP = BP)

高校数学a 図形の性質 内接円と接線まとめと問題
円の性質 接線
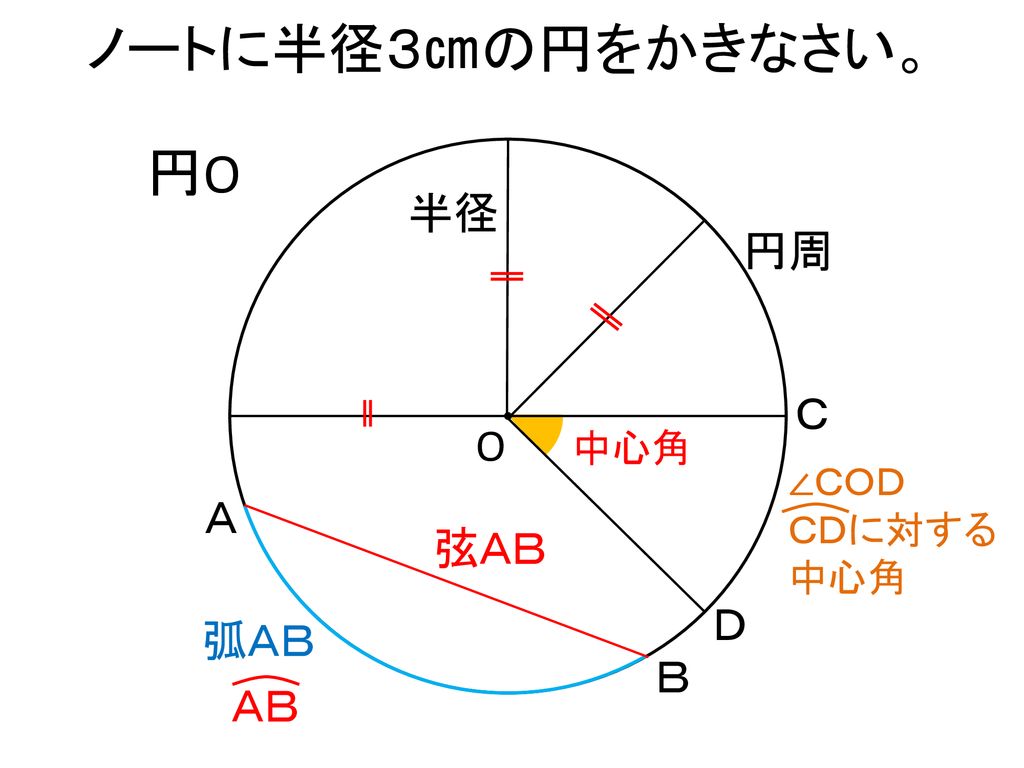
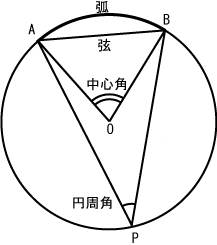
円の性質 接線- 放物線の直交する2本の接線の交点の軌跡は放物線の準線になることが知られている これに対応し,\ 円\ x²y²=a²b²}を{双曲線の準円という 双曲線の準円は,\ 元の双曲線の漸近線によって上下左右の4つの部分に分割される円の性質 弦と弧 円周と2 点で交わる直線を割線という。 このときの交点を 2 点 a, b とするとき、円周によって、割線から切り取られる線分 ab のことを弦といい、弦 ab と呼ぶ。特に円の中心を通る割線を中心線という。中心線は円の対称軸であり、円の面積を 2 等分する。



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
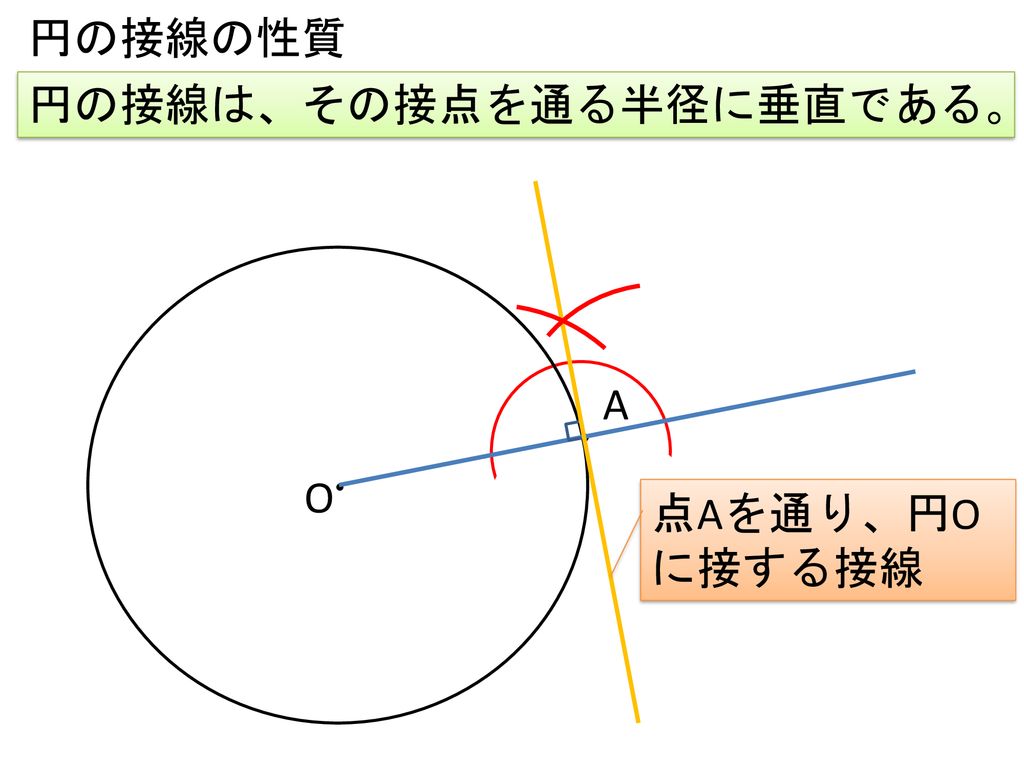
・円の接線の性質を確認する。 円の接線は ・作図方法を復習する。 円の接線の性質を板書する。 接点を通る半径に垂 直である。 ターレスの定理を復習し,板書す る。 3 課題についての説明を考える。 (30分) 課題 なぜ,このような方法で作図を行 えば ここでは、接点を $(x_1,y_1)$ としましょう。これは円周上の点でもあるので\ x_1^2y_1^2=r^2 \が成り立ちます。 接線も接点を通ります。また、接線の傾きは、円の中心と接線を結んだ線と接線とが垂直に交わることから求めることができます。円と接線において成り立つ定理について理解し、その性質を活用する練習を行なう問題プリントです。 中学生の無料学習プリント・教材プリント ログイン/新規登録(無料) こんにちは、 さん
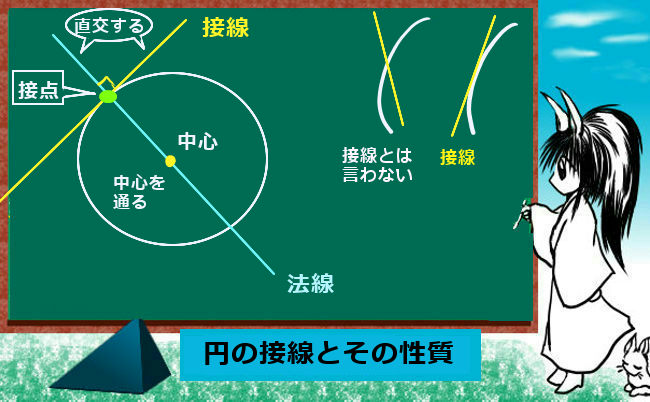
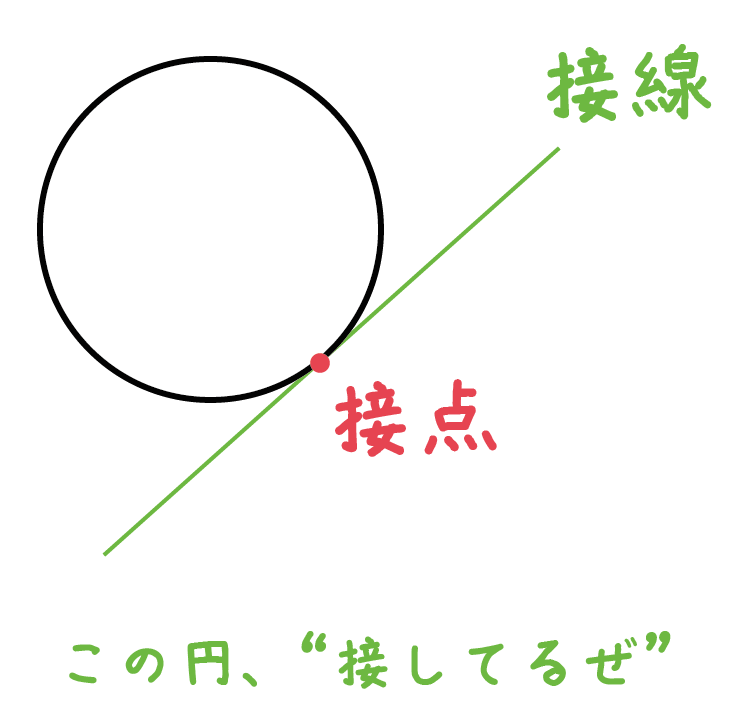
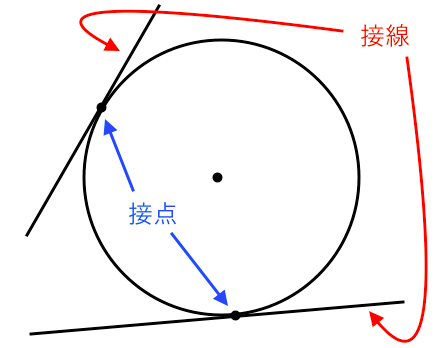
円周角の定理の極限 次に,接弦定理が成り立つことの感覚的な説明を紹介します。 点 c c c を円周上で限りなく a a a に近づけていくと, 円周角の定理より ∠ a c b \angle acb ∠ a cb は一定 直線 c a ca c a は円の接線に近づく 以上から接弦定理が成り立つことが納得できます。円の基本的な性質 弦、接線、接点という言葉は覚えていますか? その図形的性質は覚えていますか? 覚えていないとまったく問題が解けませんので、必ず暗記しましょう。 弦と二等辺三角形 円 \(o\) と円と直線が同一平面状に存在するときには, ・ 2 点で交わる ・ 接する ・ 離れている の 3 つの場合が考えられます。 ここでは接するときを考えていきます。 円に接する直線のことを円の接線といいます。 また,このときただ 1 つの共有点のことを接点 といいます。
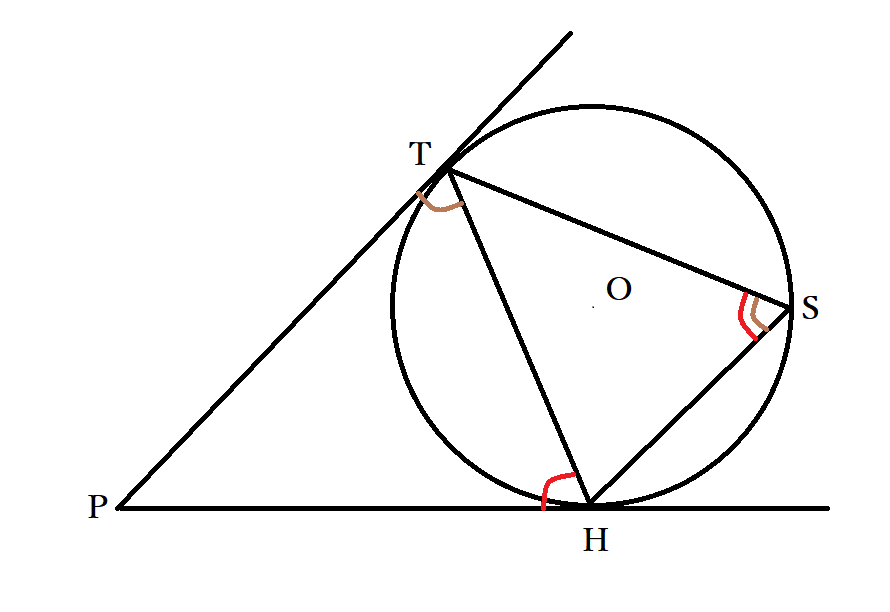
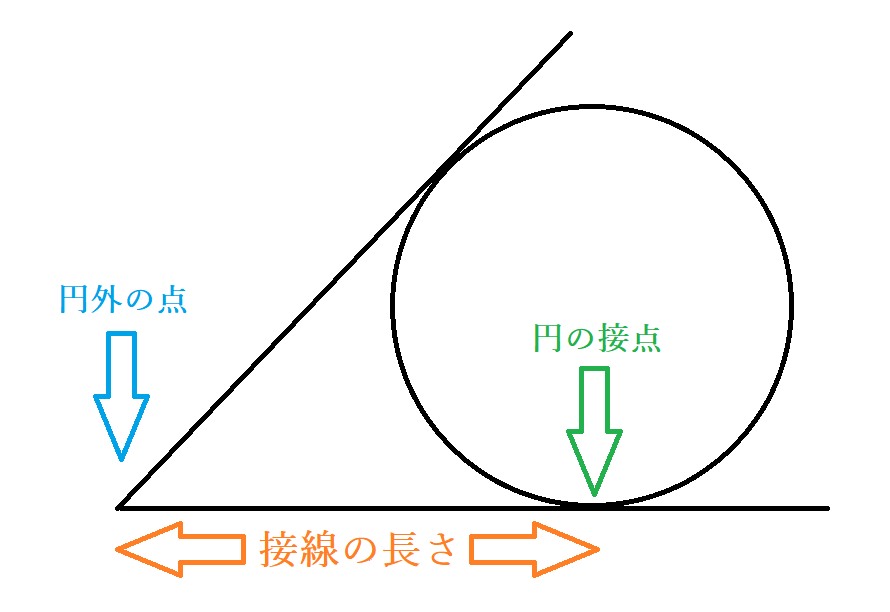
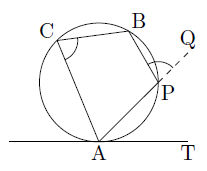
円の性質 三角形や多角形の事を学んだら次は円に移る。 円の外側のとある点からその円に接線は二つ引ける。 また、左のように点pから二つの接線を引いたとき ap=bp がなりたつ。 また、四角形の内部に円に外接するとき、 abcd=adbc がなりたつ。 という内心の場合に,性質2の導出の肝となるのは,1点から円に引いた2本の接線の長さが等しいことでした: a f = a e, b d = b f, c d = c e円oの直径abをとる。点bを通る接線と、点aと円周上の点cを結んで延長した線の交点をdとする。 abdと bcdにおいて、 円の接線とその接点を通る弦の作る角は、その角の内部にある孤に対する円周角に等しいので、 ∠bad=∠cbd 共通な角なので ∠adb=∠bdc




円の接線 数学a By Okボーイ マナペディア




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
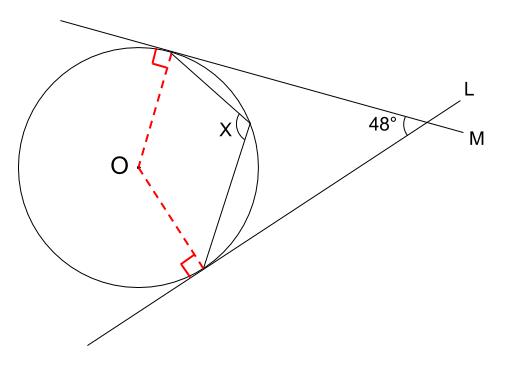
この接線を考える場合には、2円に次のような特徴があることを覚えておきましょう。 先ほどの接線の作図を理解できれば、こちらも同じような考え方で進めていきます。 まずはそれぞれの中心を通るような円をかきます。 その後、半径 となるような円円の接線と弦の作る角が (1)直角 (90 ), (2)鋭角 (90 より小さい), (3)鈍角 (90 より大きい) の3つの場合に分けて示すこととします. (1) BAT=90 のとき (漢字2文字を入れなさい↓) 弦ABはになるので, (数字を入れなさい↓) BCA= ゆえに.BAT=BCAが成り立ちます 円と接線の関係 以下の特徴があります。 1円の接線( m m )は接点を通る半径に 垂直 である。 2円外の点( B B )から、その円に引いた 接線の長さ(BA = BC B A = B C ) は等しい。



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



中3数学 円の性質15 円と接線 すべて無料 星組の中学数学講座
接線の長さに関する問題を、三平方の定理や図形の 相似を利用して考える 2 ②円と相似 円と交わる直線でできる図形の性質を円周角の定理 と図形の相似を利用して考える。 2 円周角の定理の利用 三角形に内接する円の半径を求める。2円の交点を通る円の方程式 → 携帯版は別頁 原点を中心とする円の接線の方程式 円 x2y2=r2 の円周上の点 ( p , q) における接線の方程式は p x q y=r2 (1) 例1 ___円 x2y2=25 の円周上の点 (3 , 4) における接線の方程式は3x4y=25 今回は、こんな質問をいただきました↓点(4, 6)を通り、円 (x -1)2 (y - 1)2 = 9 に接する直線の方程式は?この問題、直接書いてないですが、円の接線を求める問題です。円の接線を求める問題には、与えられる条件によって、




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
接線と弦のつくる角の定理の証明 では、なぜこのような定理が成り立つのか。 簡単に確認しておきましょう! なぜ、次のような位置にある角の大きさが等しくなるのでしょうか。 これを考えるには、まず 接点から、直径になるように線を引いて 下の 外接円の半径の公式 公式①正弦定理から求める 公式②3 辺と面積から求める 外接円の半径の求め方例題 外接円の性質 性質①外心(外接円の中心)と垂直二等分線 性質②外心と各頂点との距離 外接円の書き方 外接円の練習問題 円と接線に関する3定理(垂直、接線の長さ、接弦定理) スポンサーリンク 高校数学A 平面図形 検索用コード 円の接線は,\ 接点を通る半径と垂直をなす 円の外部の点から引いた2本の接線の長さは等しい 接点を通る弦と接線が作る角は,\ その角




中学校数学 3年生 図形 円 Wikibooks
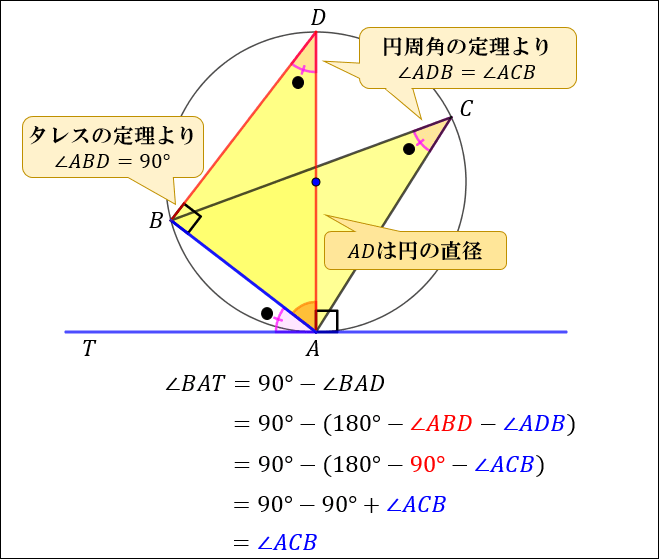



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
また、この直線を円の 接線 (tangent line, tangent) といいます。 円と接線との共有点を、 接点 (point of tangency) といいます。 円の接線の方程式・公式 円の接線の方程式・公式は超重要なので必ず覚えましょう。 円の接線の方程式・公式(X-A)2 (Y-B)2 = R2 上の点 (X1, Y1)の円の接線の方程式・公式 ⇒ (X1-A) (X-A) (Y1-B) (Y-B)=R2 ※特に、中心が (0, 0)の円の方程式 ⇒ X1X Y1Y = R2 2円の接線の方程式に関しては,円周上の点t1 と原 点oを結ぶ直線と,t1 を接点とする円の接線が直交 する(円の接線は接点を通る半径に垂直である)性質 を用いて,数学Ⅱの「図形と方程式」において導



数学a 平面図形 円の性質 2つの円の共通接線



高校入試 英語 数学 円周角の定理の応用
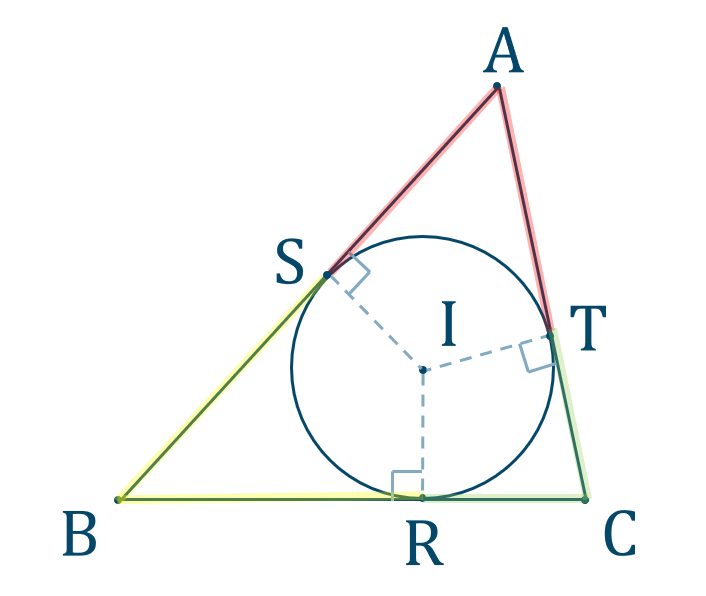
「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように 円と2点で交わる直線を引いて 、円と直線の 交点を点A、点B とします。 円の中心を点O 、 直線ABの中点を点M とします。 内接円の性質 内接円には、大きく \(2\) つの性質があります。 性質①内心と各辺の距離 多角形のそれぞれの辺が内接円の接線となっていて、各接点から引いた垂線の交点が内接円の中心(内心)となります。円外の点から引いた接線 タイプ: 教科書範囲 レベル: ★★ 円の外部の点から引いた接線を扱います. 円の接線の公式 が既習である前提です. 解法が複数あるので,ここで整理します. 目次 1: 円外の点から引いた接線の求め方 2: 例題と練習問題




中3数学 円の性質12 接線と弦のつくる角 接弦定理 すべて無料 星組の中学数学講座




接線と円の関係 Jsciencer
-円の接線の性質を理解し,接線の作図ができるようになろう-p161,162 学習日 月 日 年 組 番 氏名 作図に使用した線は消さないこと。 1 次の各問に答えなさい。 (1) 次の空らんにあてはまることばを書き なさい。 ・ 下の図のように,円の中心を通る直線 このように 「原点が中心の円」 で 「接点が ( x 1 − a, y 1 − b) である接線の方程式」 を考えることになります。 ここがミソです。 そうすると先ほど私たちが覚えた接線の公式が使えて ( x 1 − a) x ( y 1 − b) y = r 2 とできますね。 あとは 円を元の位置円と直線 三角形と円 接線の長さ 2円の位置関係 2円の共通接線 同じ弧に対する円周角 円周角の定理の逆 円に内接する四角形



中3数学 円の接線ってどんな性質があるの 子育てに役立つ情報メディア ママコティービー
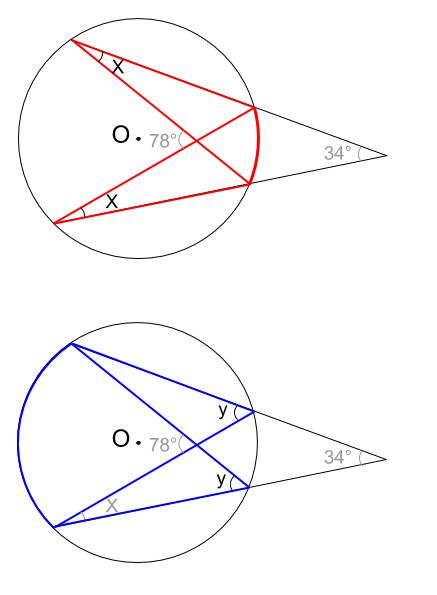



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



世界一わかりやすい数学問題集中3 6章 円の性質




高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月



1




中学校数学 3年生 図形 円 Wikibooks
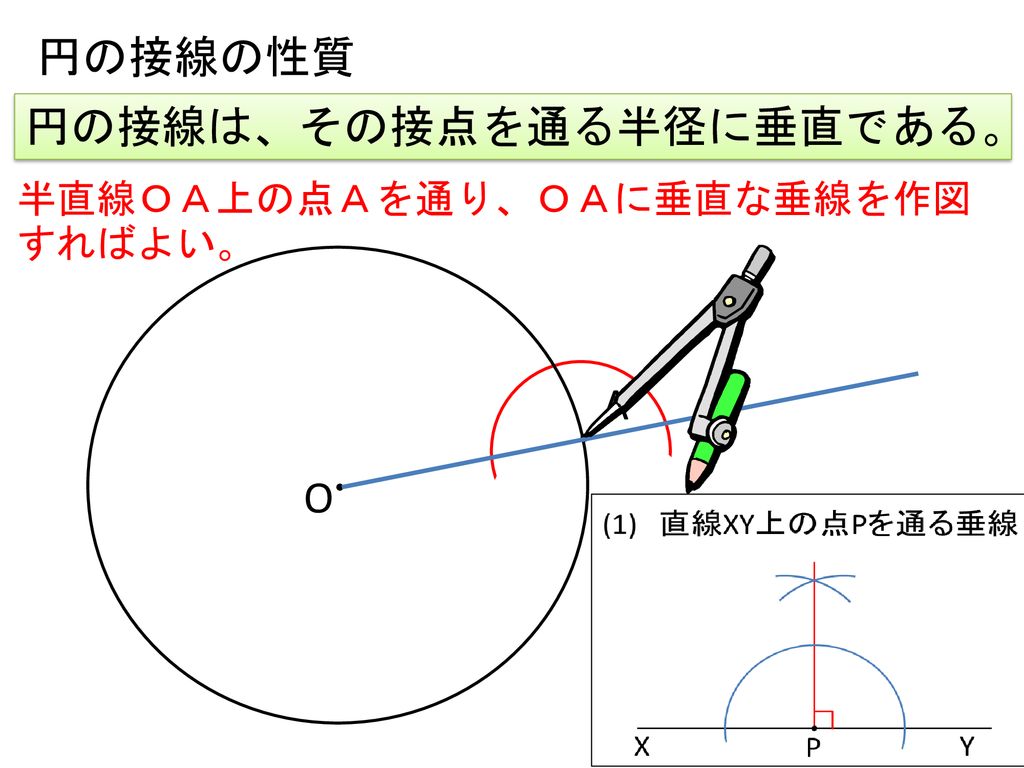



本時の目標 円の性質と 円と直線の関係を理解する 円の接線の作図をすることができる Ppt Download
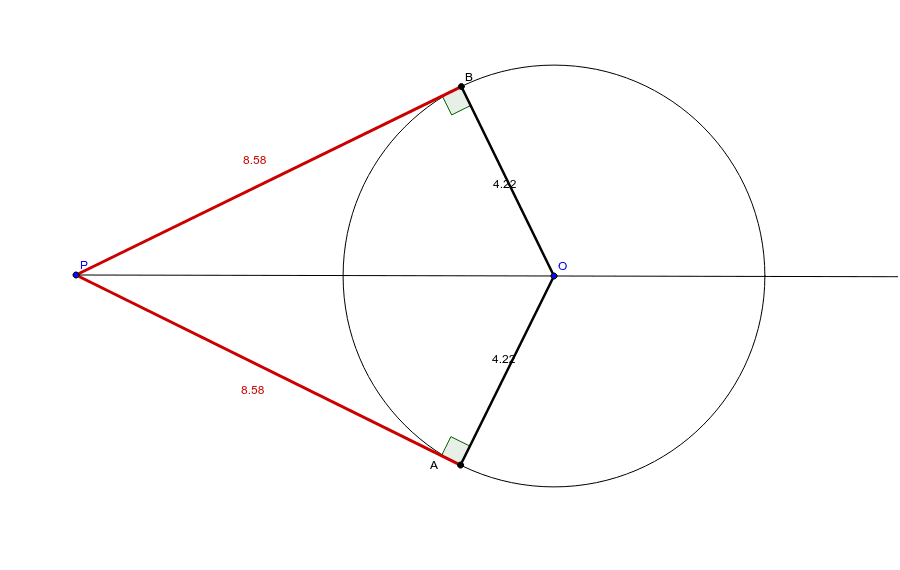



円の接線 接線の長さ Geogebra




接弦定理の証明 円周角が鋭角ver 数学a By となりがトトロ マナペディア




中学 高校までの円に関する定理や性質をまとめました 平面図形 高校生 数学のノート Clear
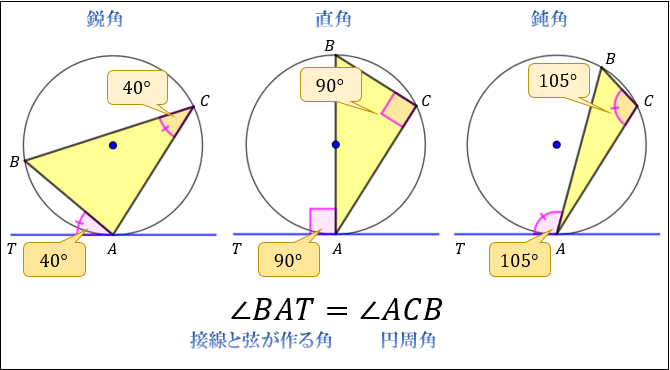



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
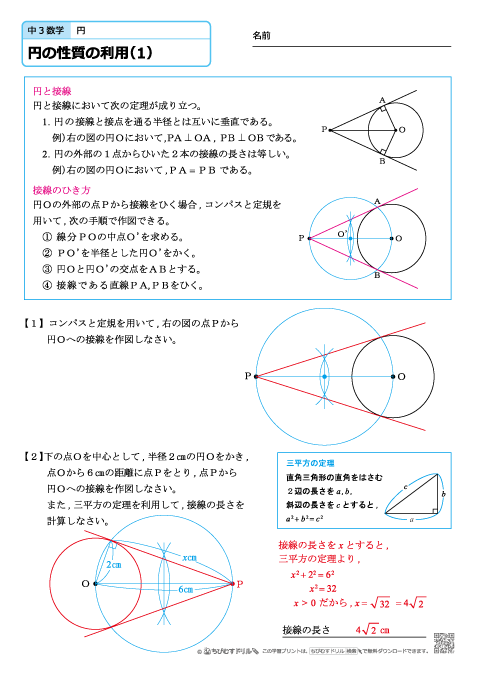



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
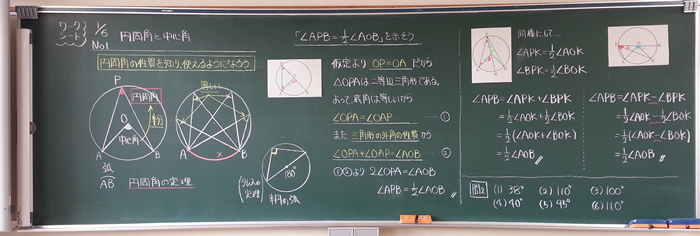



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館




図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん




高校数学a 接線と接線の長さ 練習編 映像授業のtry It トライイット
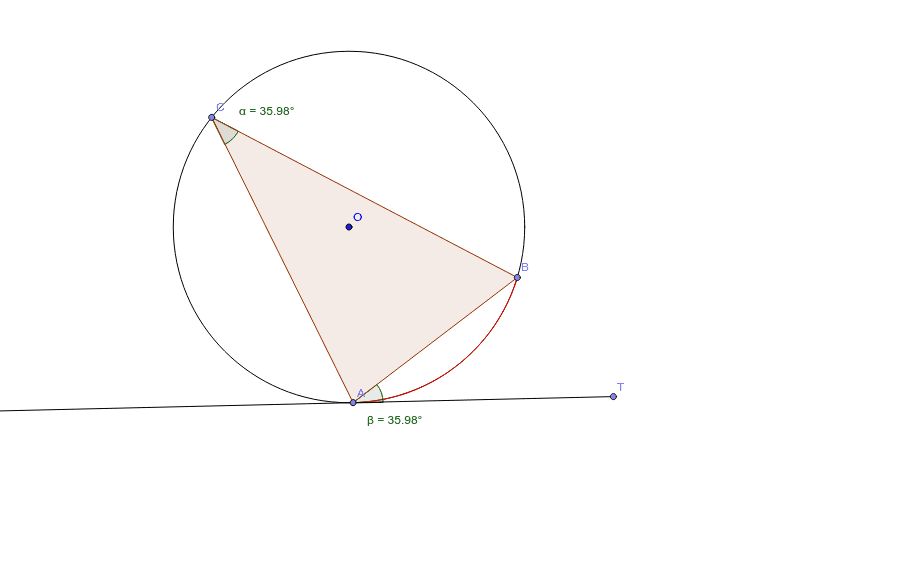



接線と弦の作る角 Geogebra




原田 浩明 Pa Twitter Sサクシード059 円の接線の長さ 接弦定理 接線と弦の作る角の定理 高校 数学 1年 数学a 図形の性質 定理の証明




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円 数学 Wikipedia



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



方べきの定理の証明と例題 思考力を鍛える数学




高校数学a 図形の性質 内接円と接線まとめと問題



円の接線と内接 外接 理数系無料オンライン学習 Kori




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




高校数学a 図形の性質 内接円と接線まとめと問題



1
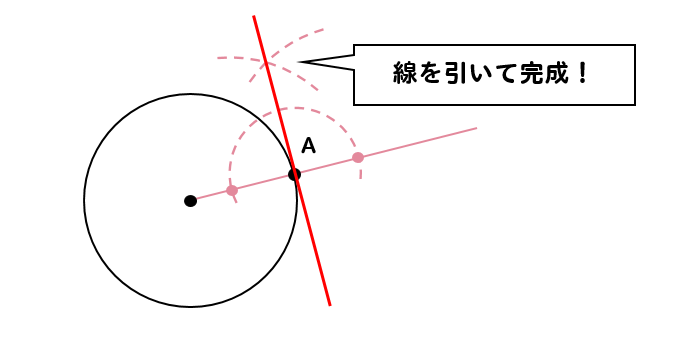



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ



数学a 平面図形 円の性質 2つの円の共通接線
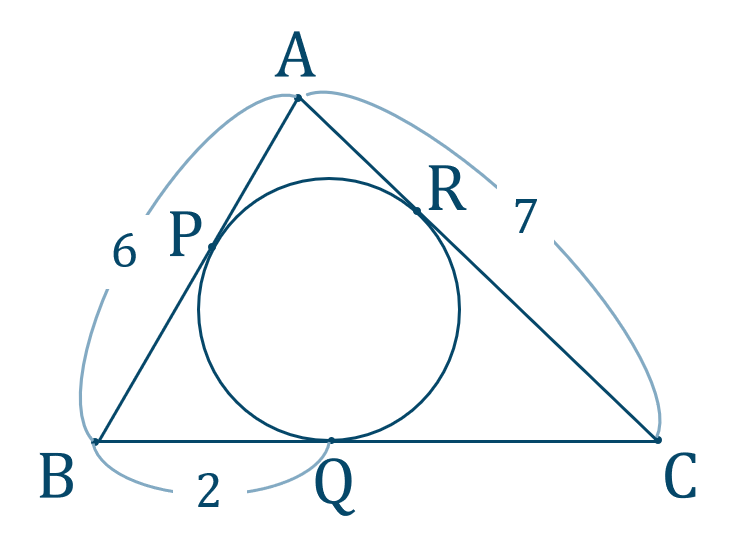



数学a 内接円と接線の条件の使い方とコツ 教科書より詳しい高校数学




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円と接線 教遊者




2円と共通接線 数学a フリー教材開発コミュニティ Ftext
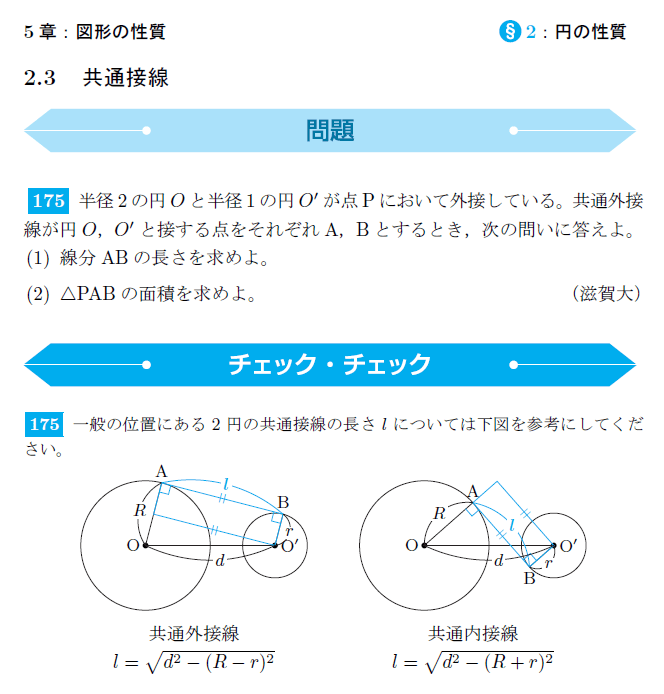



数学 図形の性質 共通接線 さくらの個別指導 さくら教育研究所 Skredu



Ten Tokyo Shoseki Co Jp Spl Hl Support Files Kou 319 Ef A1 Af Af 2 E7 Ab A0 2 E7 Af 80 E5 9b E5 81 Ae E6 80 E8 Pdf




接線と弦のつくる角の定理 問題の解き方 証明をサクッと解説 数スタ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




高校数学a 共通接線の長さを求める問題 例題編 映像授業のtry It トライイット



Math 高校入試の難問 円と接線 働きアリ The 2nd




円と接線 中学3年生 円の性質 数学 Youtube




接線と円の関係 Jsciencer




2円と共通接線 数学a フリー教材開発コミュニティ Ftext
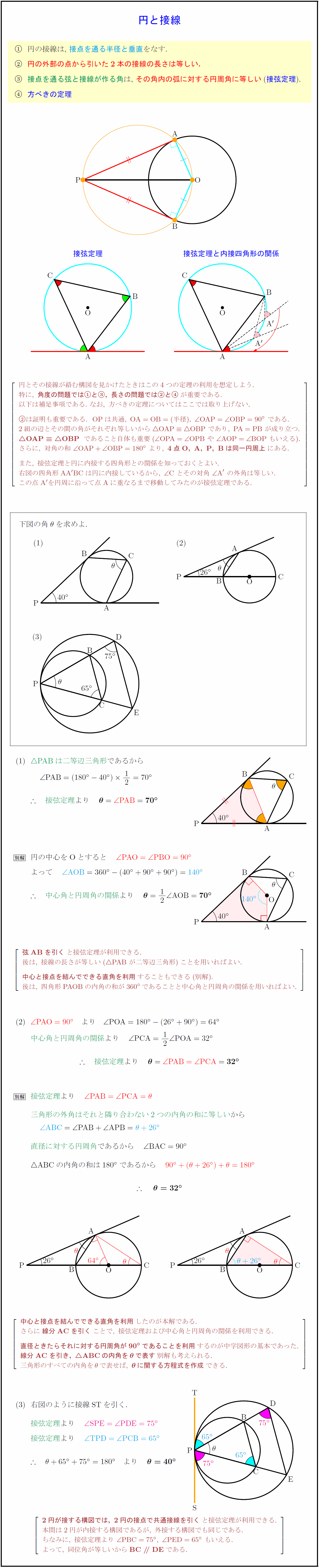



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月




連質本当に本当にsorryでございます 1枚目 1 合ってますか Clear
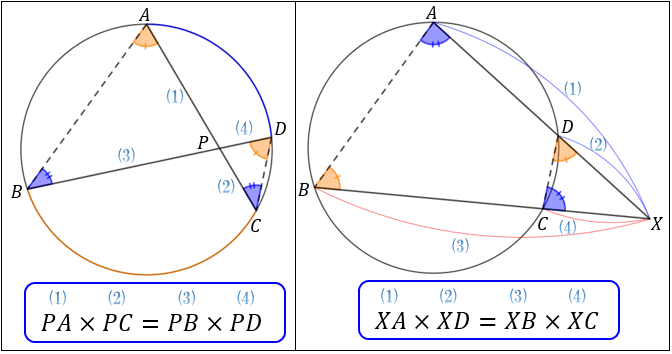



方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
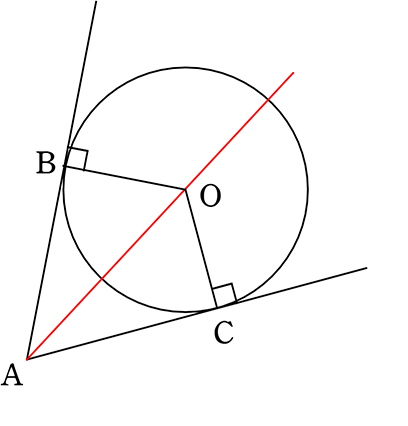



中学数学 円周角 中心角




世界一わかりやすい数学問題集中3 6章 円の性質



円の接線と角度 中学から数学だいすき
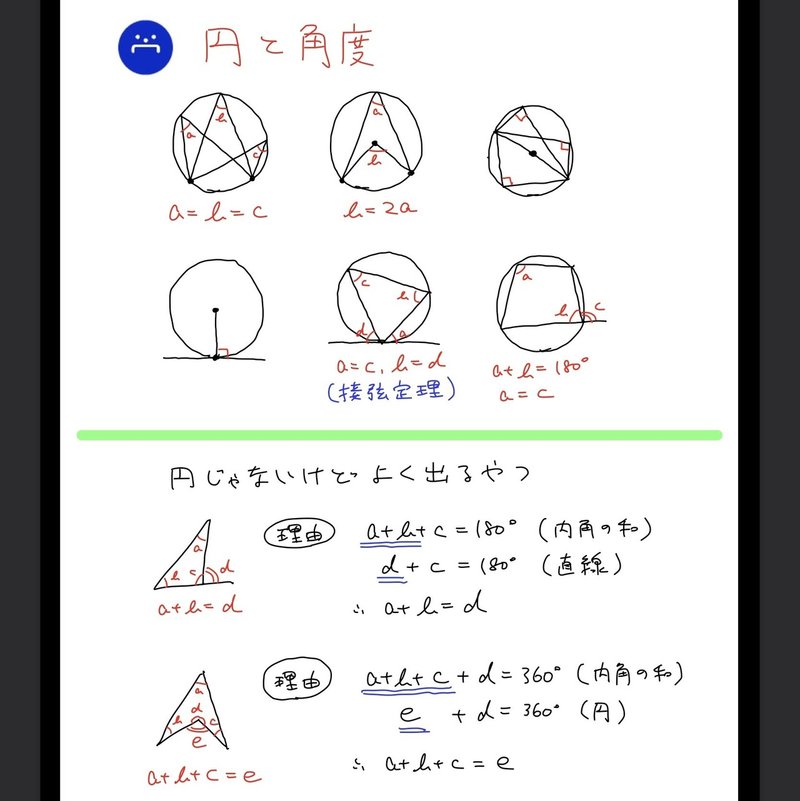



高校数学無料問題集 数a 第2章 図形の性質 円に関する問題 桝 ます Note



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




図形の性質がわかません 図の Oebが90度になる理由がわかりません Okwave



本時の目標 円の性質と 円と直線の関係を理解する 円の接線の作図をすることができる Ppt Download



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



接線と接点について知ろう 苦手な数学を簡単に




これ説明してくれる人いますか なんでこうなるのか分かりません Clear



円 に関するチャートを作ってみました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




基本 円の接線の方程式 なかけんの数学ノート
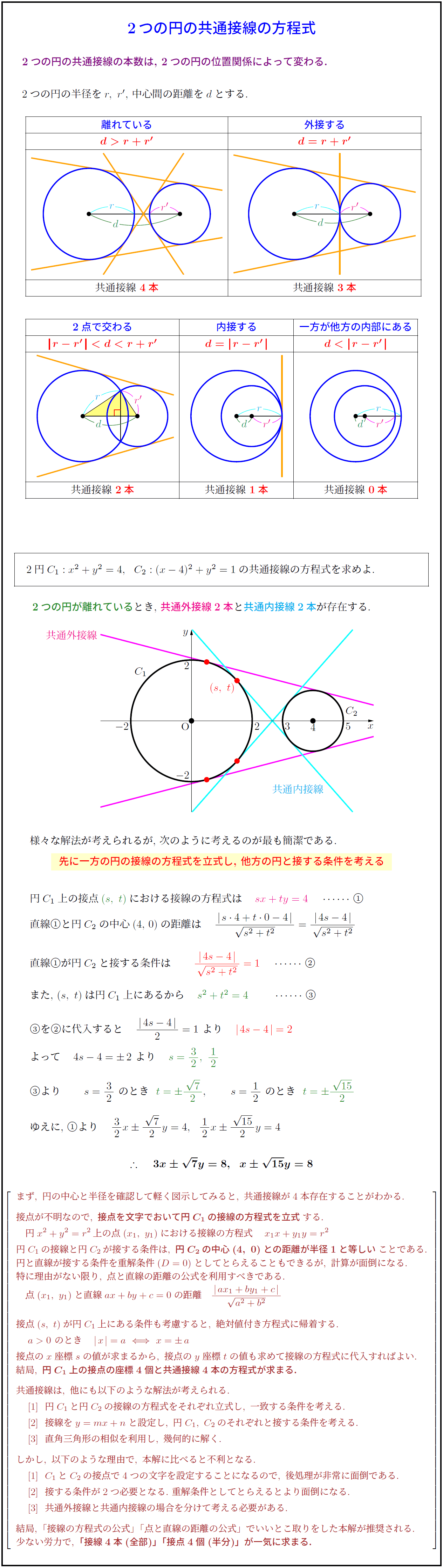



高校数学 2つの円の共通接線の方程式 受験の月
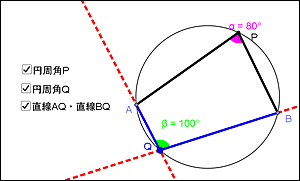



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館
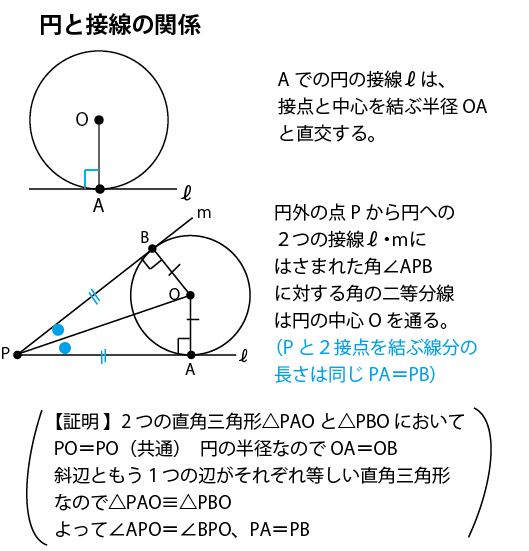



17年前期 千葉県公立高校入試数学 第2問 5 作図 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
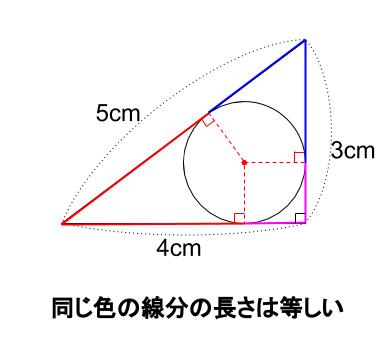



三角形の内接円 中学数学の無料オンライン学習サイトchu Su




知ってると得 円の接線の作図 円に接する円の作図方法 はてなラボ




円の接線の長さの証明 数学a By となりがトトロ マナペディア




中学数学 円と接線 Youtube
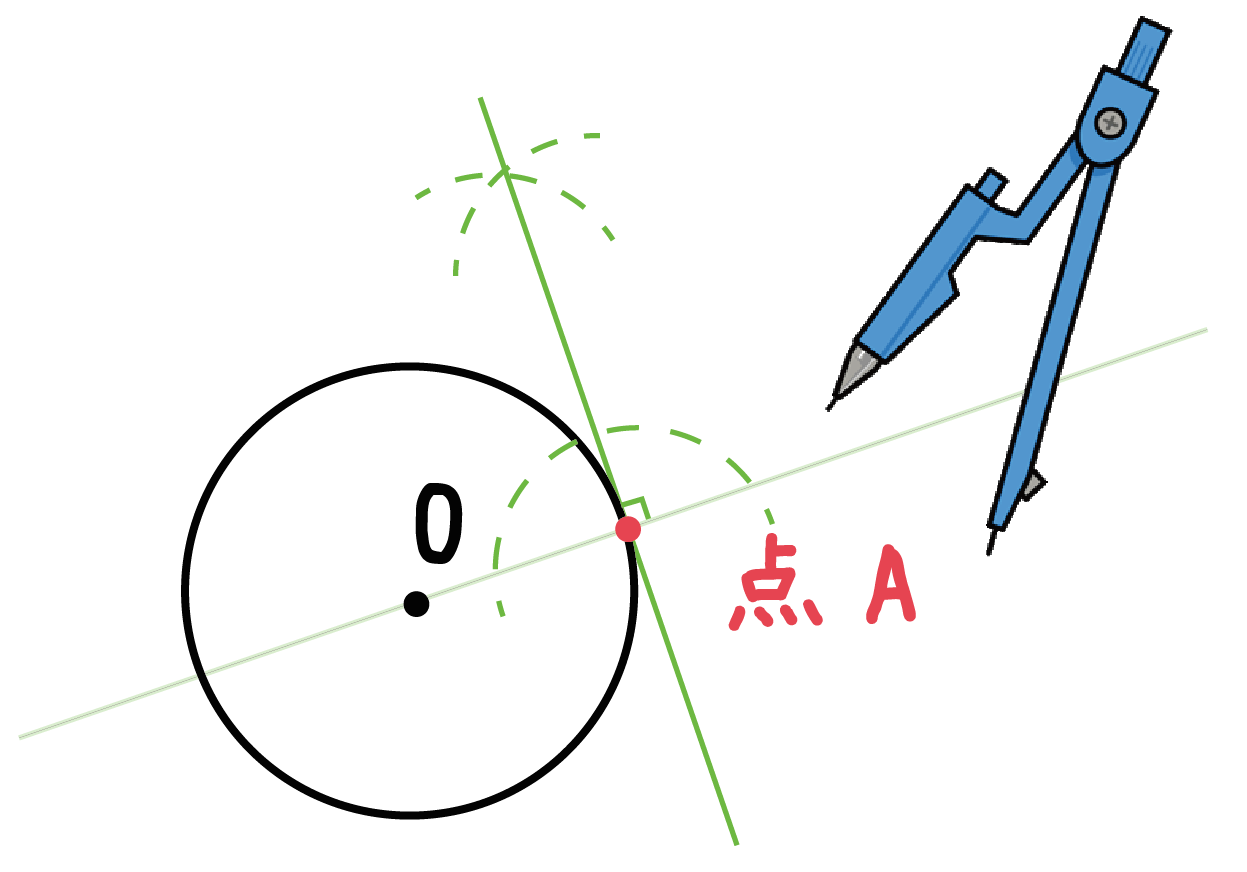



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



接弦定理 まなびの学園
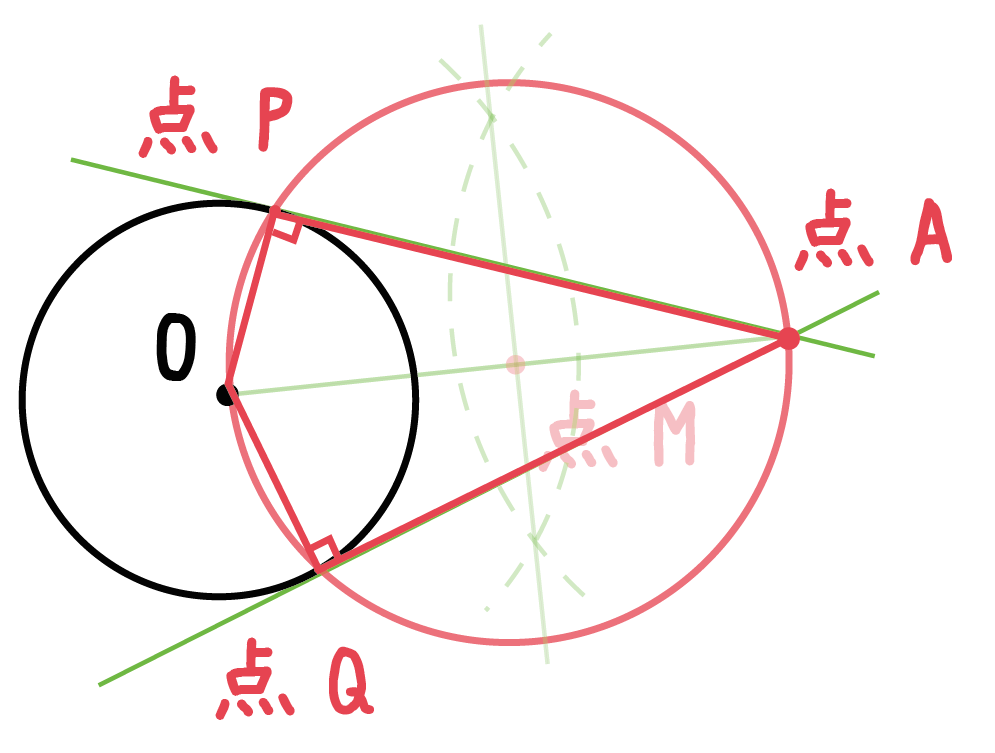



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



本時の目標 円の性質と 円と直線の関係を理解する 円の接線の作図をすることができる Ppt Download



接弦定理
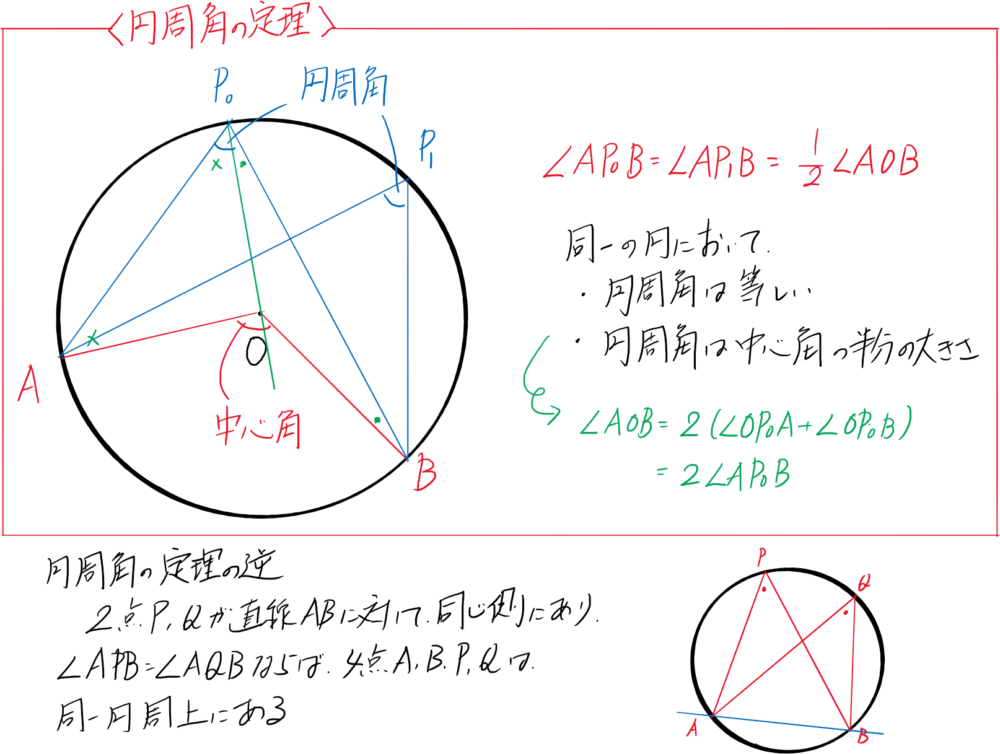



円の性質 円周角の定理 平面幾何 富岡市の総合学習塾 トータルアカデミー
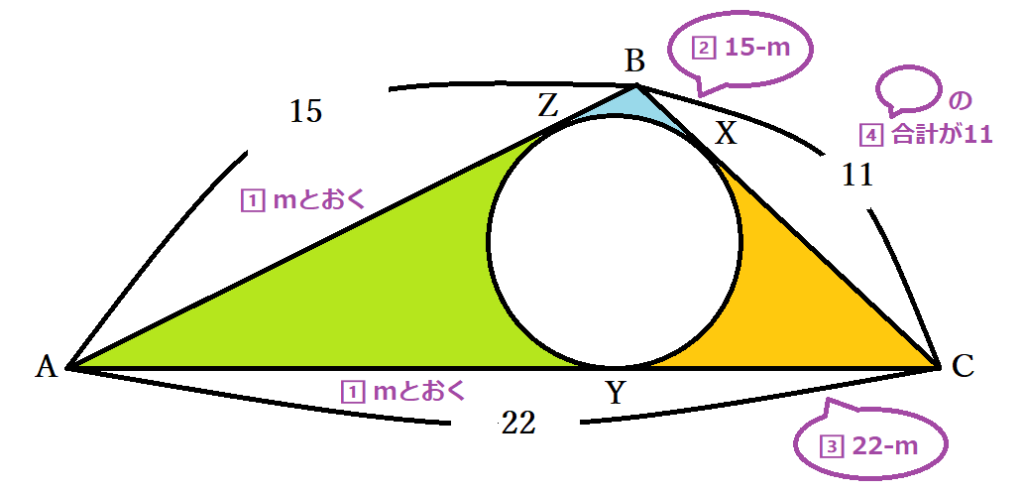



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



3




接線と弦の作る角 接弦定理 無料で使える中学学習プリント




くろべえ 円の接線
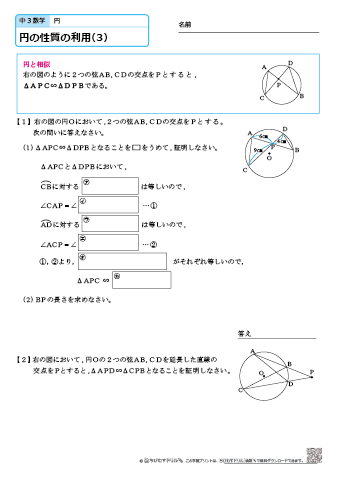



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生



数学a 平面図形 円の性質 円の接線




2つの円の共通接線の長さの求め方 数学の偏差値を上げて合格を目指す
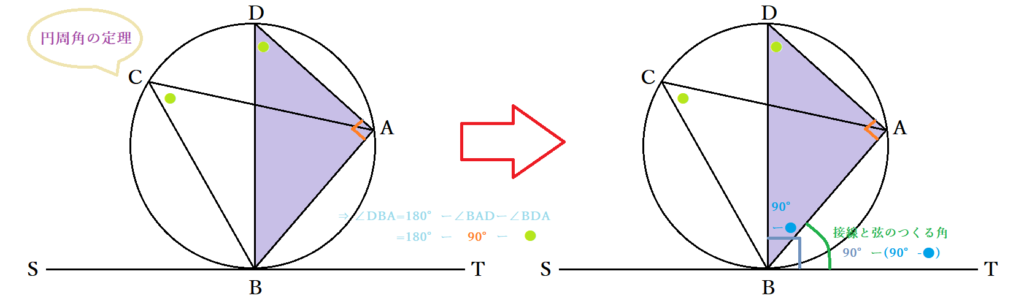



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




高校数学a 接弦定理1 基本 映像授業のtry It トライイット



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典
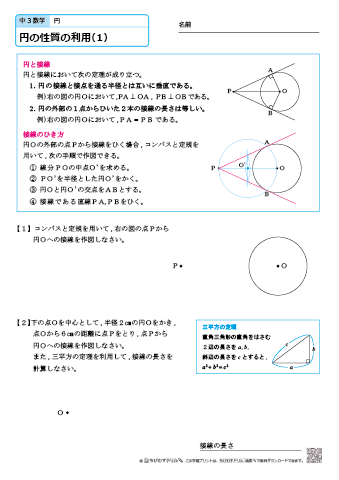



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生



1



円 数学 Wikipedia
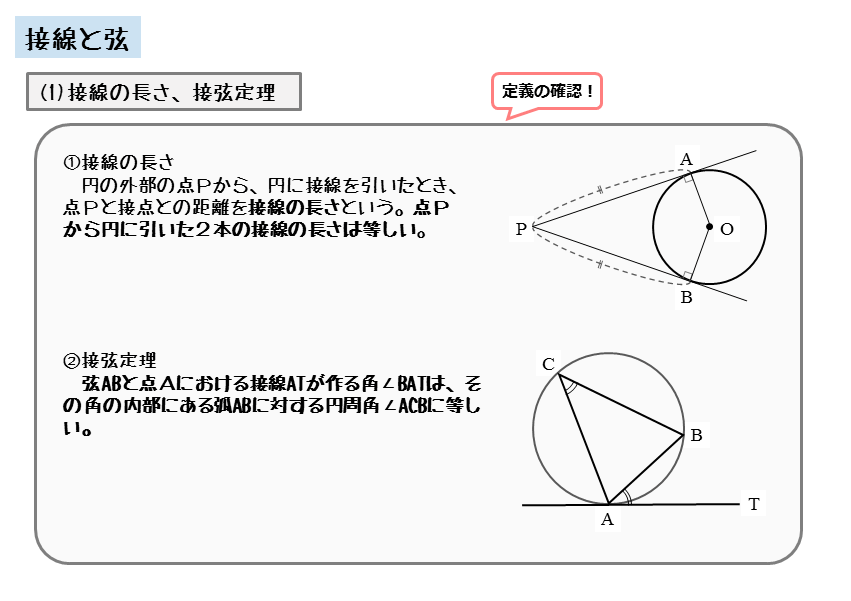



図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん




中学数学 円周角 中心角




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
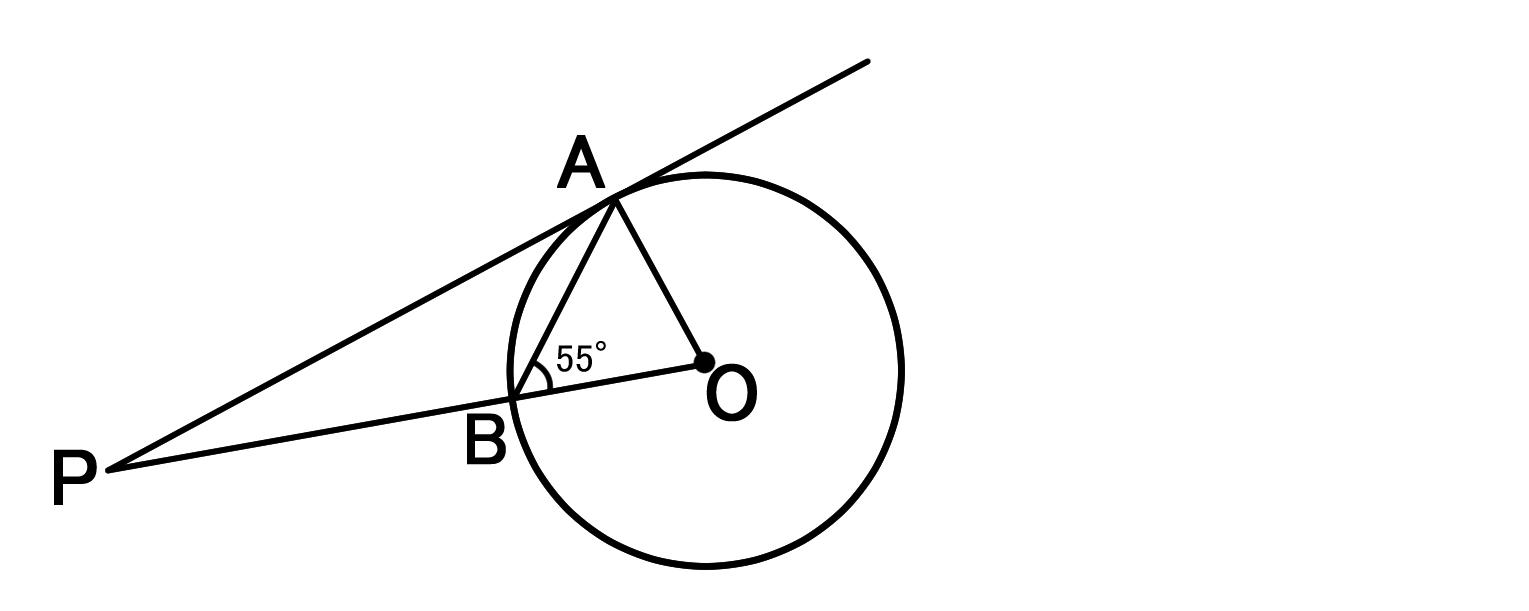



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



0 件のコメント:
コメントを投稿