正方形面積算法 274112-正方形面積算法

Google Scholar provides a simple way to broadly search for scholarly literature Search across a wide variety of disciplines and sources articles, theses, books, abstracts and court opinions這種蒙特卡羅算法的原理是：如果隨機樣本一致地散布於一個包含圓的正方形中，樣本擊中圓的比例趨近於圓和正方形的面積比。 這可以視為求圓（或任何區域）面積的最後一種手段，因為它要求巨大的樣本數才能確保精確度，一個 10 − n 的估計需要大約 100 n正 方 體 有 6 個 面 ， 每 一 個 面 都 是 正 方 形 ， 且 其 面 積 都 一 樣 大 。 所以表面積＝ ＝ ＝ 。 所 以 表 面 積 ＝ 5 × 5 × 6 ＝ 25 × 6 ＝ 150 。 答： 平方公尺。 答 ： 150 平 方 公 尺 。 寫成公式為： 寫 成 公 式 為 ： 正方體表面積＝邊長 邊長

正方形面積計算公式 正方形的面積等於邊長的平方 S A A 正方形面積計 百科知識中文網

正方形面積算法

正方形面積算法-三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。影片：觀念認識正方體的體積公式，數學 > 主題式 > 國小 > 空間與形狀 > 立體形體 > 五年級正方體與長方體體積。源自於：均一教育平台 願 每個孩子都成為終身學習者，成就自己的未來。

正方形面积求边长算法 微页高考网

如图所示，这 4个 led 122，124，126，128可以排列为基本正方形或者矩形的图案，并且位于控制器 110的 r1和 l1按钮之间的桥接上。 図示するように、4つのled122、124、126、128は実質的に正方形または長方形のパターンで配置されてもよく、rlボタンとllボタンの間のコントローラ110のブリッジ部にこのパラドックス「面積1はどこから来たか？ 」 は、有名な フィボナッチの数列 の特徴を応用しています。 このことについて詳しくお知りになりたい方は、私の別のサイト： フィボナッチ数列とリュカ数列 をご参照ください。算しているため．同面積のモデルa，b，dの分布の 総量（分布の積分量）が等しくならないことに注意 する必要がある．まず図3をみると同面積の正方形 b（s／l＝0．43）よりも面積も4つの長方形の距

如何计算正方形的对角线 正方形的对角线是连接两个对角的线段。要算出其对角线长度，你可以用公式d = s\sqrt{2}，其中的s表示正方形一条边的边长。但是，有时题目只会给出正方形的周长、面积等其他值，让你根据这些值来求对角线长度。在这些情况下，你必须先用其他公式来算出边长，然后再この八角形は、面積が9の正方形5つと面 積が9／2 の三角形4 つで構成されている。 したがって、八角形の面積は63 となる。63 は1 辺が8の正方形の面積64 に近似する。 このように考えると、直径9の円の面積はお よそ64となる。 この円の半径は9／2 である。ユ緒 言 正方形あるいは矩形照射野の場合に,組 織/空 中線量比(TAR)を その照射野の周囲の長さP に対する面積Aの 比ぐA/P)の 関数で表わすと,両 対数グラフ表示で直線となることをSterl

15年（サレジオ学院中学 5秒後に直角三角形ABCと正方形DEFGが重なる部分の面積を求めなさい。 → 解答 （問題6） 対角線の長さが8cmの正方形を1つの頂点を中心に図のように45 回転させました。 黒くぬった部分の面積を求めなさい。四邊形的面積 蔡聰明 一 問題的提出 給一個三角形, 已知三邊長, 那麼它的 面積可用著名的 Heron 公式來求算。 這我們 在"談Heron 公式 記一段教學經驗"一文 中, 己經有所敘述1。 現在要加以推廣, 我們 自然想到了兩個方向 (i) 維數的提高, 從平正方形 efgh の面積は言うまでもなく, です。ところが, この面積は, 正方形 abcd から, 薄青で塗られた直角三角形を取り除いた面積と等しいはずです。すなわち,

正方形面积公式

長方形面積教案日期 Txbnx

 传说是古代的 叙拉古 国王 希伦（ Heron ,也称海龙）二世发现的公式，利用三角形的三条边长来求取三角形面积。 但根据Morris Kline在1908年出版的著作考证，这条公式其实是 阿基米德 所发现，以托希伦二世的名发表（未查证）。 我国宋代的数学家 秦九韶 也正方形是特殊的平行四边形，也是特殊的长方形。在同一平面内：四条边都相等且一个角是直角的四边形是正方形 3 。 有一组邻边相等的矩形是正方形。 有一个角为直角的菱形是正方形。 正方形对角线相等以下图为例： 比如我想把面积第2小的那个"小正方形"选择出来，算法代码如下： 该实现算法的关键是对算子tuple_sort_index意思的理解。 代码中： Area = 4, 12

正方形面積計算公式 正方形的面積等於邊長的平方 S A A 正方形面積計 百科知識中文網

三年級數學一道面積周長題 優秀生都錯成這樣 其他同學呢 壹讀

正n 角形の面積を一般的に計算しておきます． 2 これを用いて「全ての頂点が格子点にある正n 角形が存在したとすると，n = 4 になること」を 証明します 3 逆にn = 4 ならば，全ての頂点が格子点にある正4 角形を実際に描けることが図1 や図2 から分 かり開平法の原理 与えられた正の数の正の平方根の小数表示を求めるために、ここではまず漸化式を立てて、一般的な求値法を求める。 そして、求値の明確化のために、開平法と呼ばれる筆算の原理を導出する。 以下は十進法表示の場合だが、他の位取り記数法でも同様な計算で求められる。我們都知道正方形面積算法是「邊長 2 =邊長×邊長=面積」。 因此，如果√2 代表正方形面積為 2 的邊長，那麼 (√2)2 就會是在算 這個正方形面積，也就是 2，我們就可以寫出下面的等式 (√2)2= √2×√2=2。 從這個等式，我們可以觀察到兩件事：

102上中數2年級教學簡報1 1乘法公式

长方形面积怎么算长方形的面积有几种算法 不规则的长方形怎么算面积

前ちゃんの中学校数学の部屋：授業実践事例一覧 授業実践事例一覧 プレゼン教材実践 自作教具実践 学び直し実践 他の実践 「主体的・対話的で深い学び」実践例 単元／内容 授業開き 思考力・表現力を鍛える授業ネタ 話合いや小テストに役立つ此页面最后编辑于年3月18日 (星期三) 1133。 本站的全部文字在創用CC 姓名標示相同方式分享 30 協議 之條款下提供，附加條款亦可能應用（請參閱使用條款）。 Wikibooks®和維基教科書標誌是維基媒體基金會的註冊商標；維基™是維基媒體基金會的商標。 維基媒體基金會是在美國佛羅里達州登記方形瓷砖合并算法 我有一个8x8方形板，可以有不同颜色的square瓷砖的任意组合。这些方形瓷砖可以具有不同的尺寸，我们可以具有从1到8的边的正方形，由于电路板的尺寸，8是最大值。 我需要找到一种算法，使我可以使用与区域本身一样大的方形瓷砖替换相同颜色的方形区域。

1

正方形面積對角線2 1 Rimbt

 正八边形：八条长度相等的线段，每个内角都是135°，首尾相连构成的一个封闭形状的平面图形。 正八边形周长的算法：边长长度乘以8。 用直尺和圆规画正八边形的方法： 1）做正方形abcd，并做正方形外接圆o e g 精(6) 如右圖,已知abcd 為正方形,bdef為長方形,bdgh為 平行四邊形,a點在ef上,h點在cg上。設正方形abcd 、長方形 bdef、平行四邊形 bdgh的面積分別為a、b、c 平方單位,則a、b、c的大小關係為 _av='/ d f h b正方形的周長是它的邊長的4倍。 如果邊長為a，那麼周長 = 。 正方形的面積是其邊長的平方。 如果邊長為a，那麼面積 = 。 如果我們知道正方形的對角線長d，那麼我們也可以之計算面積 = ，如果正方形邊心距為r，外接圓半徑是R，那麼 = 。 ， = 。 若正方形的邊長為整數，其面積就是一個完全平方數。

常用圖形求面積計算公式 人人焦點

正方形面积求边长算法 微页高考网

This video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericom椭圆面积公式 ： S=πab 椭圆面积定理：椭圆的面积等于圆周率（π）乘该椭圆长半轴长（a）与短半轴长（b）的乘积。 椭圆面积公式 应用实例 椭圆的长半轴为8cm，短半轴为6cm，假设π=314，求该椭圆的面积。 答：S=πab=314*8*6=（cm²）る正N 角形の1辺の長さを2aとすると，pN = (N 2a)=2 = Naである．一方， 図3において，OA = 1, BC = aであるから，三角形OAB の面積は， 1 2 1 a = 1 2 a である．したがって， s2N = (2N) 1 2 a) = Na = pN (1) である．すなわち，正2N 角形の面積s2N は，正N 角形の周の長さの半分pN に等 しい．したがって，N !

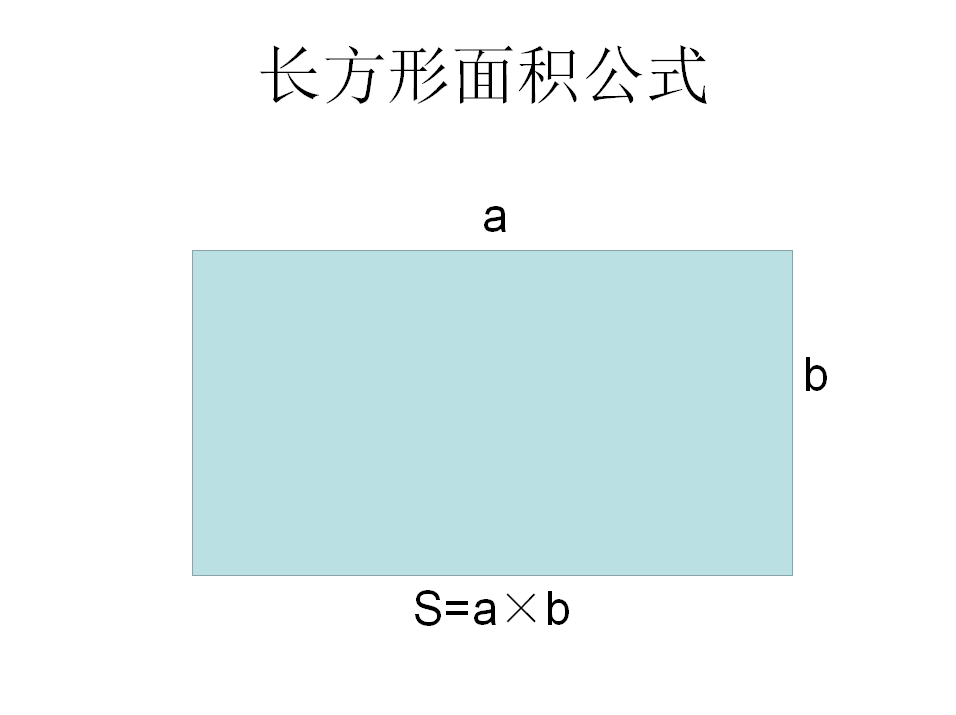
面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書

05 正方形的面積公式 Youtube

 いま、正方形Bの1辺の長さが1cmのとき、正方形Aの1辺の長さを求めてください。 ただし、両側の正方形C、Dは、同じ大きさです。 ※『算法新書』（千葉胤秀（ちば たねひで）編、文政13（10）年刊行）巻の二にある問題です。下の図のOは円の中心です。∠x，∠yの大きさを求めなさい立方公尺(m³)體積計算機， 可以使用公制單位或英制單位（英吋，英呎，碼，公分，公釐或公尺）， 除了答案還提供計算公式以及動態立方的體視覺效果， 利用這個線上小工具，可幫助我們快速來計算答案并輕鬆理解計算過程。平成18年度出題問題②中級問題&解答例 台形の中に図のように円が内接しています。 ABの長さは6cm、DCの長さは2cmで、∠ABC=∠BCD=∠90°です。 このとき円の直径は、何cmでしょう。 ※一関の和算家千葉胤秀（ちば たねひで）編集した『算法新書』（文政13

3种方法来计算正方形的面积

正方形面積計算正方形面積 Wjklv

A： 磁磚尺寸換算片數法 一坪 = 平方公分 用 ÷ 磁磚的長度 (cm) ÷ 磁磚的寬度 (cm)= 1 坪使用片數 例如 選購 30cm × 60cm 磁磚 計算法為÷30÷60=18(片) 市場常見磁磚尺寸表 (單位 公分) 10*10= 每坪使用 324 片 (密貼狀況下) 75*15 = 每坪使用 2 片 10*= 每坪使用162 片正方形 面积 = a 2 a = 边长 矩(长方)形 面积 = 宽 × 高 w = 宽 h = 高 平行四边形 面积 = b × h b = 底 h = 垂直高度 梯形 面积 = ½（a b） × h h =垂直高度 圆形 面积 = π × r 2 周长 = 2 × π × r r = 半径 椭圆形 面积 = π ab 扇形 面积 = ½ × r 2 × θ r =半径 θ=角度（以弧度このurlは、「正方形 扇形 面積 ステップ1 面積を求める① 17 次の図1は正方形の中に正三角形を2個かいた図形で、図2は正方形 の中におうぎ形を4個かいた図形です。このとき、次の問いに答えなさ い。 ⑴ 図1のアの角度を求めなさい。

103 4 21表面積的解法 小巫小屋 隨意窩xuite日誌

如何使用qgis計算多邊形面積和周長 How 21

本記事は、数学定数である円周率の歴史（えんしゅうりつのれきし）について詳述する。 円周率 π は無理数なので、小数部分は循環せず無限に続く。 さらに、円周率 π は超越数なので、その連分数表示は循環しない。 その近似値は何千年にも亘り、世界中で計算されてきた。 梯形要百比平行四边形，长方形，正方形范围都广，平行四边形，长方形，正方形其实都是梯形的特殊情况。 梯形性质： 1，梯形的上下两底度平行； 2，梯形的中位线（两腰中点相连的线问叫做中位线）平行于两底并且等于上下底和的一半。いま、正方形Bの1辺の長さが1cmのとき、正方形Aの1辺の長さを求めてください。 ただし、両側の正方形C、Dは、同じ大きさです。 ※『算法新書』（千葉胤秀（ちば たねひで）編、文政13（10）年刊行）巻の二にある問題です。

Teacher Hsieh 的教學園地 面積的計算

长方形与正方形面积计算 二 面积计算 奥数网

25 4正方形

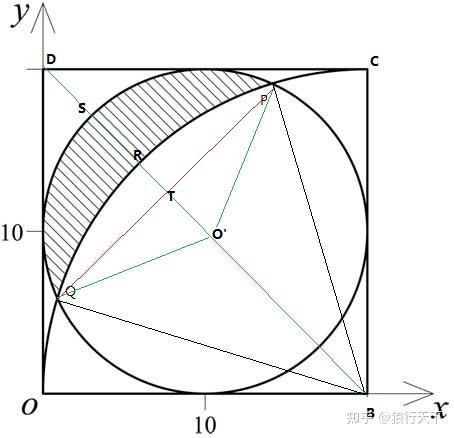
正方形边长怎么求面积 正方形面积求边长算法 正方形的边长公式

典型例题

正方形的面积公式是什么 正方形面积算法 合抱木装修网

長方形周長求面積一個長方形和正方形的面積都是1225平方米一個圓的面積是1256平方米 這三個圖形的周長 Duph

正方形面积公式小升初数学题求正方形面积 长方形和正方形的公式

Fountain 自學 小三春季課程week 10 幾何08 面積 公式算法

正方形面积求边长算法 微页高考网

腾讯视频

初中數學幾何圖形常用面積算法 趕緊收藏 每日頭條

小學數學人教版三年級下 長方形 正方形面積的計算 學案 每日頭條

一個複雜的面積問題 4個四分之一的圓和正方形重疊 王哲國小資優數學 隨意窩xuite日誌

3 31长方形 正方形面积计算练习 哔哩哔哩 つロ干杯 Bilibili

C语言 计算正方形面积 哔哩哔哩 Bilibili

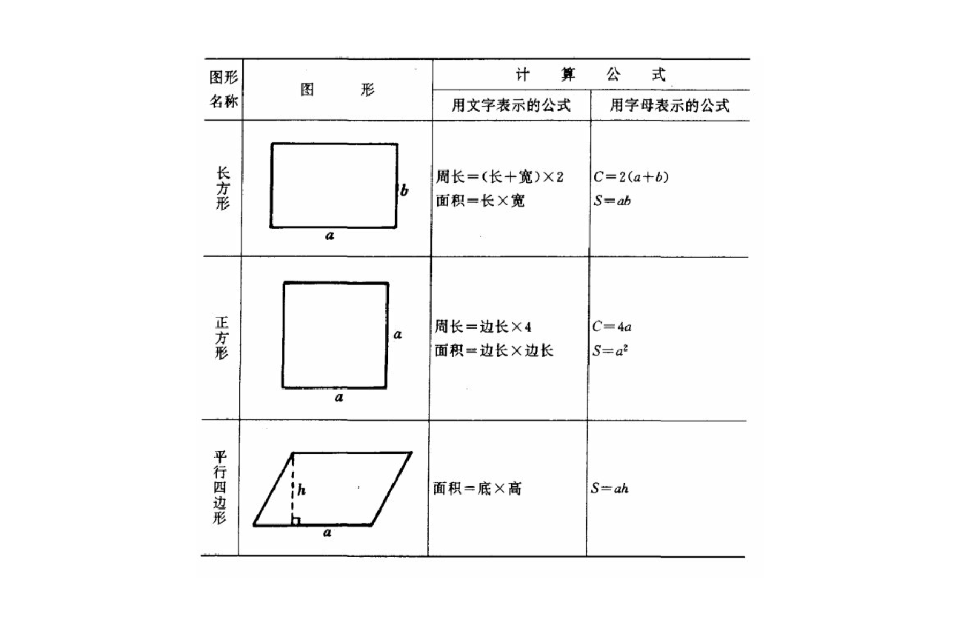
面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書

體積怎麼算 觀念 認識正方體的體積公式 Jnkz

基礎 長方形 正方形的面積公式 數學 均一教育平台

小學數學必會圖形求面積的10個方法 圖文並茂 神奇 每日頭條

25 4正方形

正方形內的蝴蝶 ５ 梅斯普雷爾的數學世界 Udn部落格

求解需要過程 Clear

1

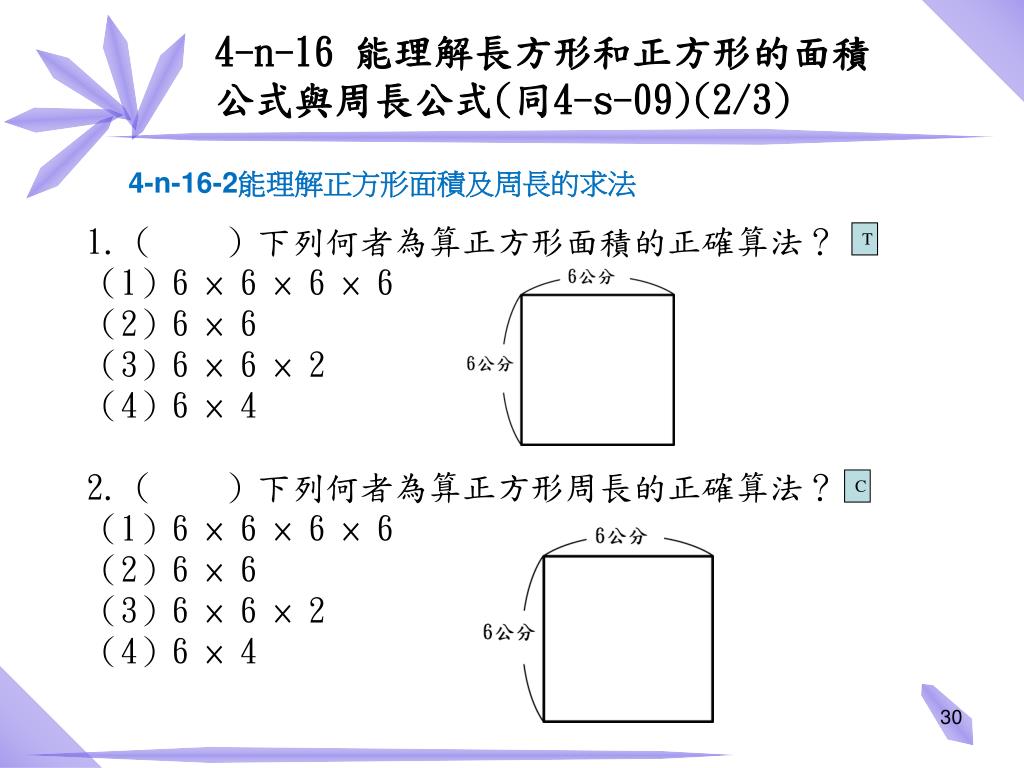
Ppt 長度與面積 授課篇 Powerpoint Presentation Free Download Id

小學必會圖形求面積10法 家長收藏版 每日頭條

正方形面积求边长算法 搜狗搜索

呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港

正方形內一點 求面積 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌

正方形面积公式

正方形面积求边长算法 微页高考网

数单位正方形求面积计算公式 视频 长方形 正方形面积的计算 可汗学院

正方形面积公式小升初数学题求正方形面积 长方形和正方形的公式

9厘米5厘米3厘米求正方形面积9厘米5厘米3厘米正方形面积是多少 答案圈

360影视 影视搜索

正方形的周长公式 长方形正方形面积和周长的公式 三人行教育网 Www 3rxing Org

例題 複合圖形的面積計算2 數學 均一教育平台

Q Tbn And9gcsrjwkdjffmnnvrpasnfv5wtndcmjpmp0l4fxggk5k Usqp Cau

长方形面积怎么算长方形的面积有几种算法 不规则的长方形怎么算面积

常用圖形求面積計算公式 人人焦點

例題 利用乘法計算面積 數學 均一教育平台

常用圖形求面積計算公式 人人焦點

Python 程式設計技巧 Apcs檢測 正五邊形面積為多少

正方形內的蝴蝶 ５ 梅斯普雷爾的數學世界 Udn部落格

正方形面积公式

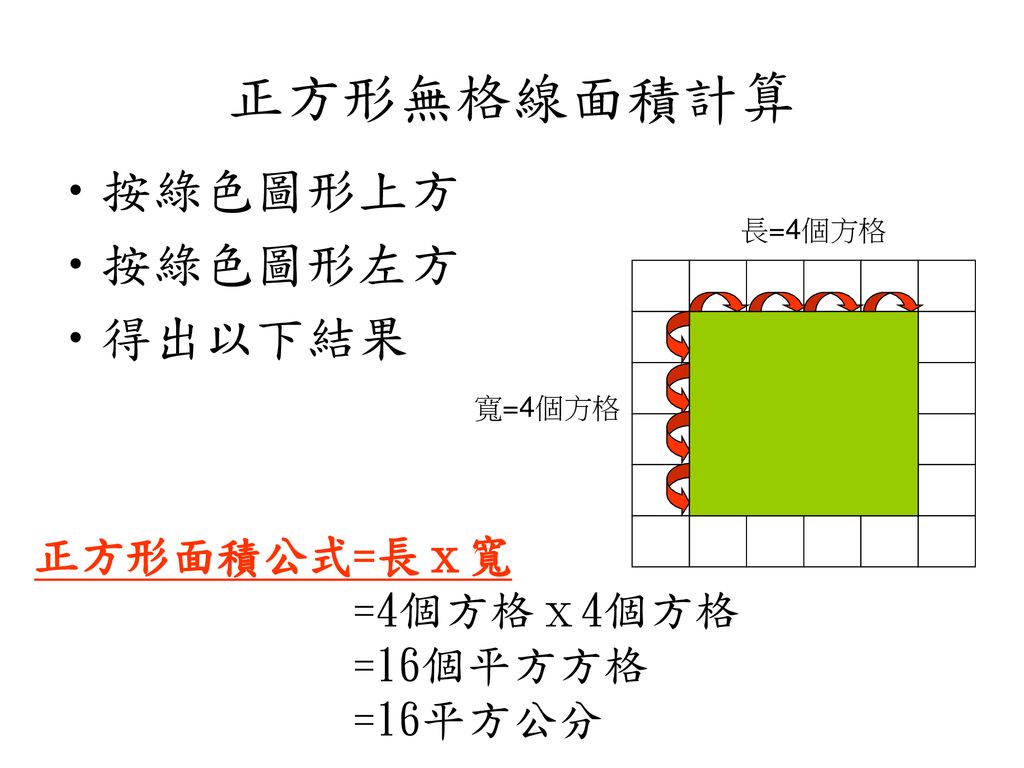
問題一假設代表1 平方公分 下圖中正方形的面積是多少平方公分 1 10 3 8 4 7 2 Ppt Download

正方形的面积公式是什么 正方形面积算法 合抱木装修网

Exam Tcte Edu Tw Examdiag Get Data Php F Getfile Pk Czozmzpcijiwmtywmnxtyxrofdn8mta1xzlmnihfbwf0af8zxzf8nfwiow Seq 0

Q Tbn And9gcrc0zk5rndihxchrex0elksjk4vngxujtpo6ofscvvgs5perp6k Usqp Cau

Www Mceducation Com Hk Cms Pri Maths Zh Supp Supp Resrc 4b 4 E4 B8 8b E9 9d E7 8d Pdf

第四講長方形 正方形的面積 每日頭條

有問有答

Teacher Hsieh 的教學園地 面積的計算

不規則圖形面積計算 每天10分鐘 奧數一點通 每日頭條

长方形面积怎么算长方形的面积有几种算法 不规则的长方形怎么算面积

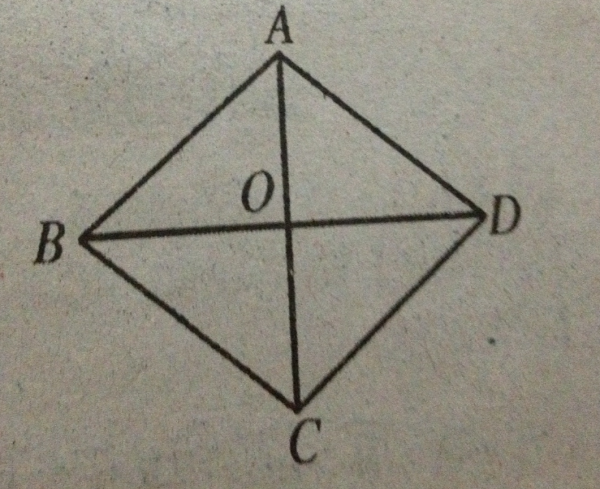
菱形面積公式 菱形面積公式 證明 中文百科全書

正方形面积求边长算法 高中数学 七千寻文化 追梦传奇人生

正方形內中心任意旋轉直角兩線段的面積計算 Wordpress Lab

面积 维基百科 自由的百科全书

3种方法来计算正方形的周长

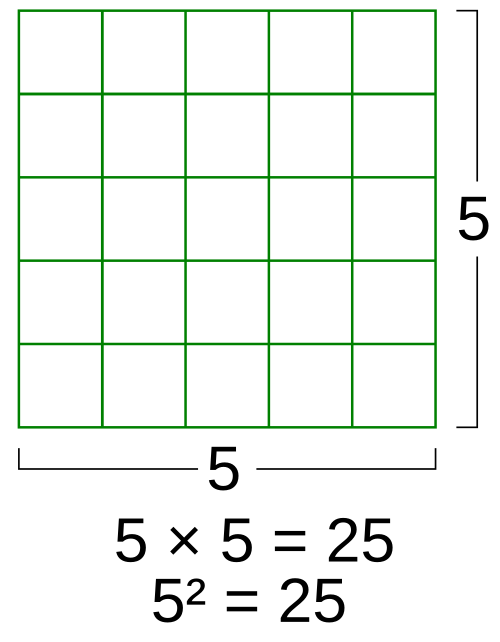
初中数学 毕氏定理 维基教科书 自由的教学读本

求圖中大正方形的面積 六年級培優題 每日頭條

長方形面積教案日期 Txbnx

求算法 ὢ Clear

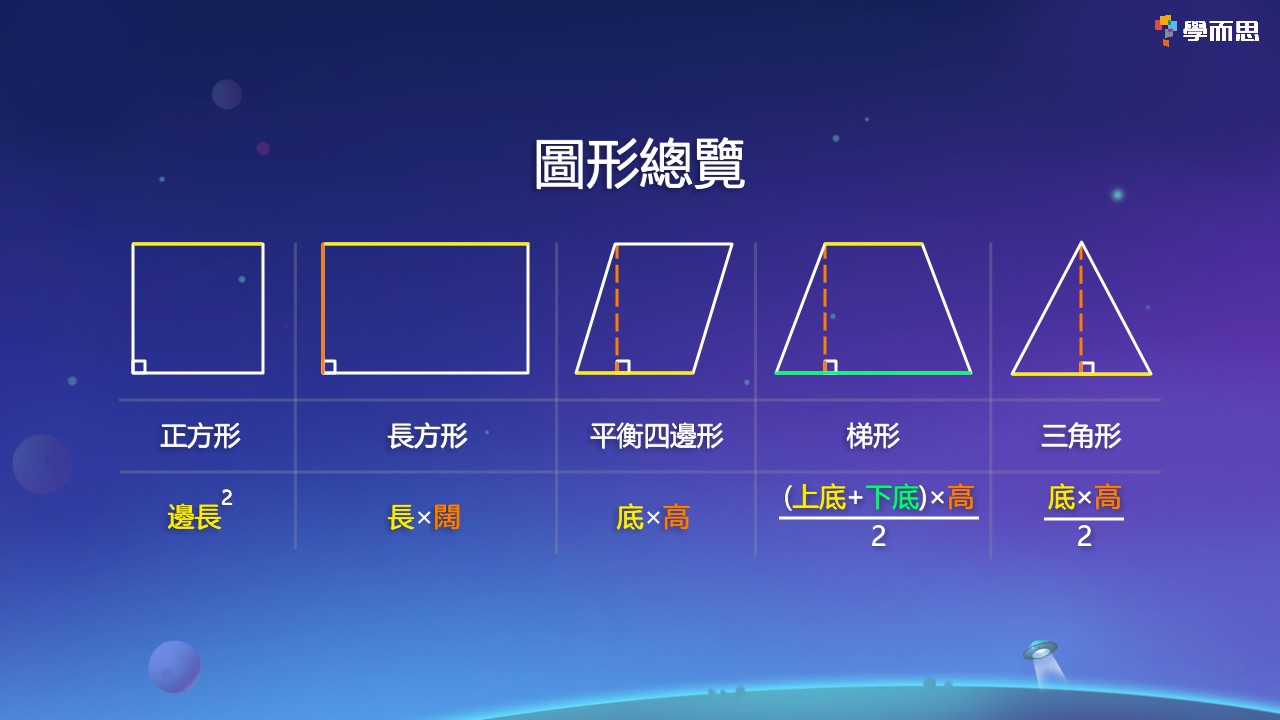
呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港

正方形面积公式

9厘米5厘米3厘米求正方形面积怎么算 抖音求正方形面积计算方法 图 特下载

問卦 國小這題面積題好難 Gossiping板 Disp s

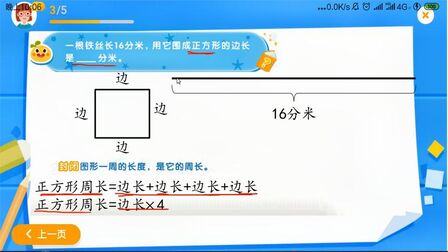
正方形面积求边长算法 搜狗搜索

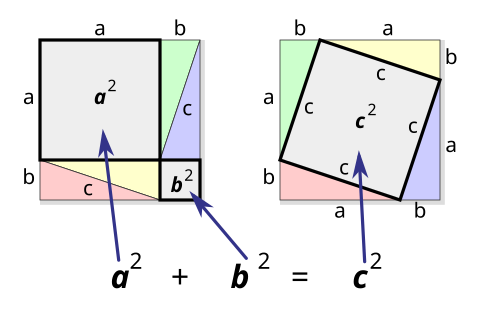
初中数学 毕氏定理 维基教科书 自由的教学读本

长方形面积怎么算长方形的面积有几种算法 不规则的长方形怎么算面积

正方形面积公式

活動二 正方形面積公式 台南市育成專案四年級數學

Python编写直角三角形边长公式 Python编程案例 模块化编程 破风的正果的博客 程序员宅基地 Python计算三角形边长 程序员宅基地

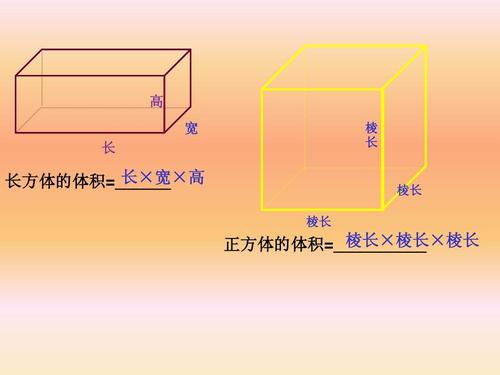
正方体面积计算公式 正方体的体积公式和正方体的表面积公式 作业帮

正方形面積換算周長正方形 長方形周長與面積 Wjklv

正方形面积公式

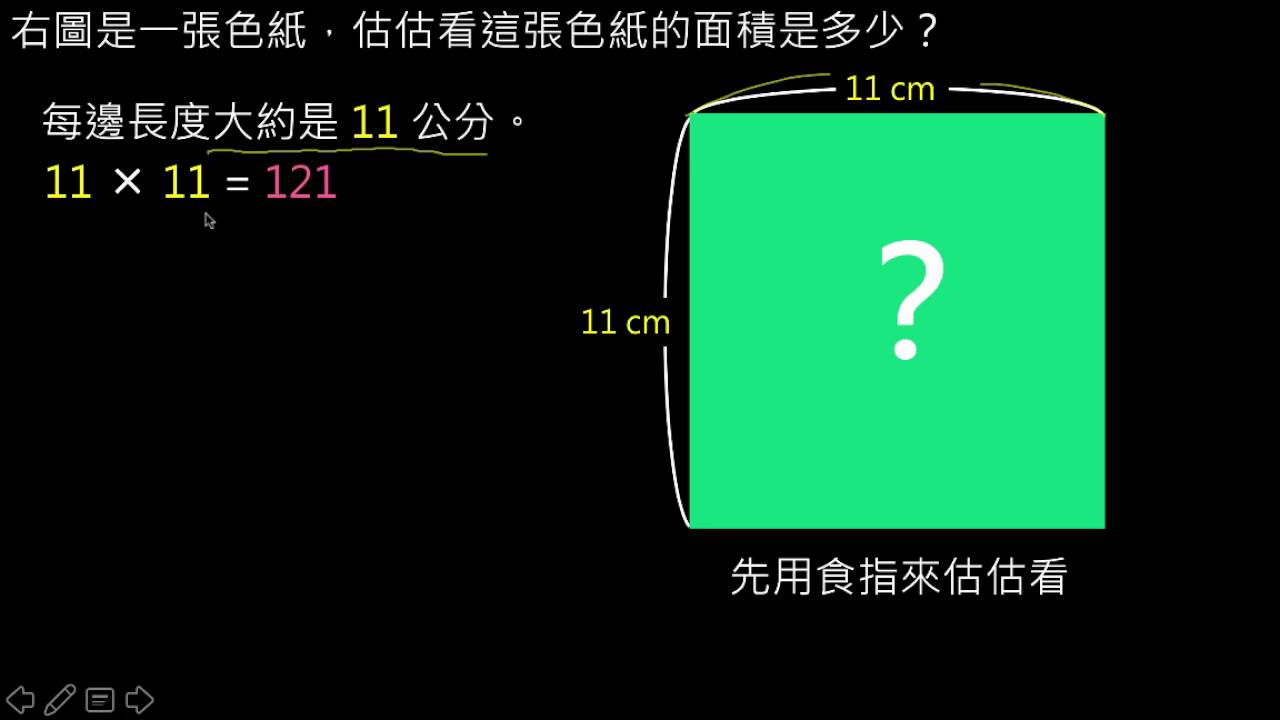
06 正方形面積公式的應用 Youtube

立體形體 18 正方體的表面積計算 Youtube

數學面積計算過程中常見的重疊問題及計算 兩圓重疊面積

3种方法来计算正方形的面积

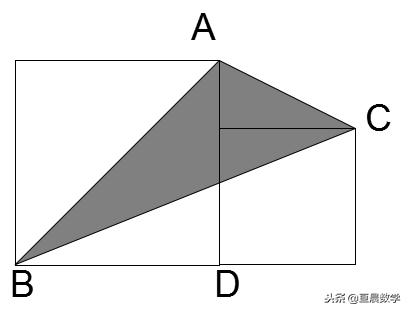
組合圖形面積計算 雪花新闻

正方形面积求边长算法 微页高考网

正方形面积公式

例題 長方形面積公式的應用 數學 均一教育平台

例題 複合圖形的面積計算1 數學 均一教育平台

正方形面积求边长算法 微页高考网

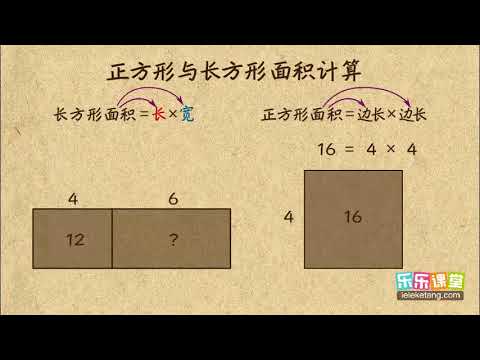
29 1 正方形 长方形面积计算小學奧數四年級幾何 Youtube

Incoming Term: 正方形面積算法,