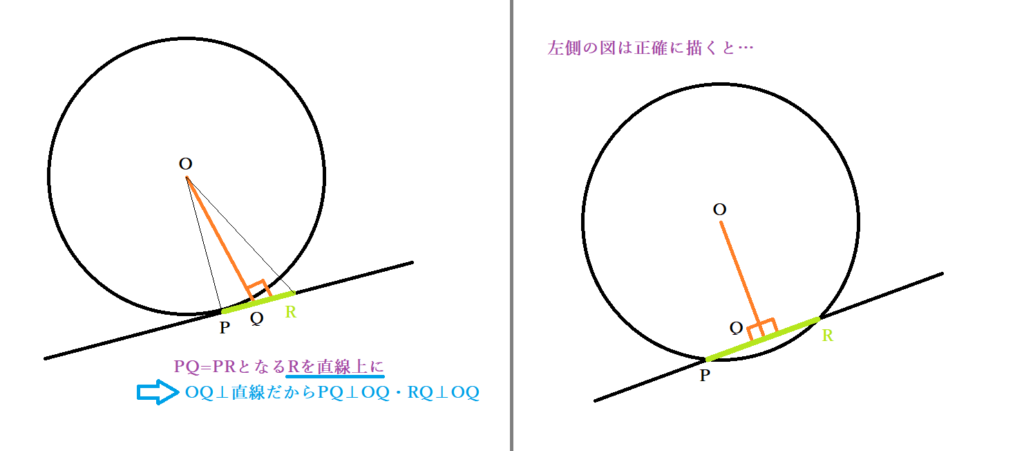
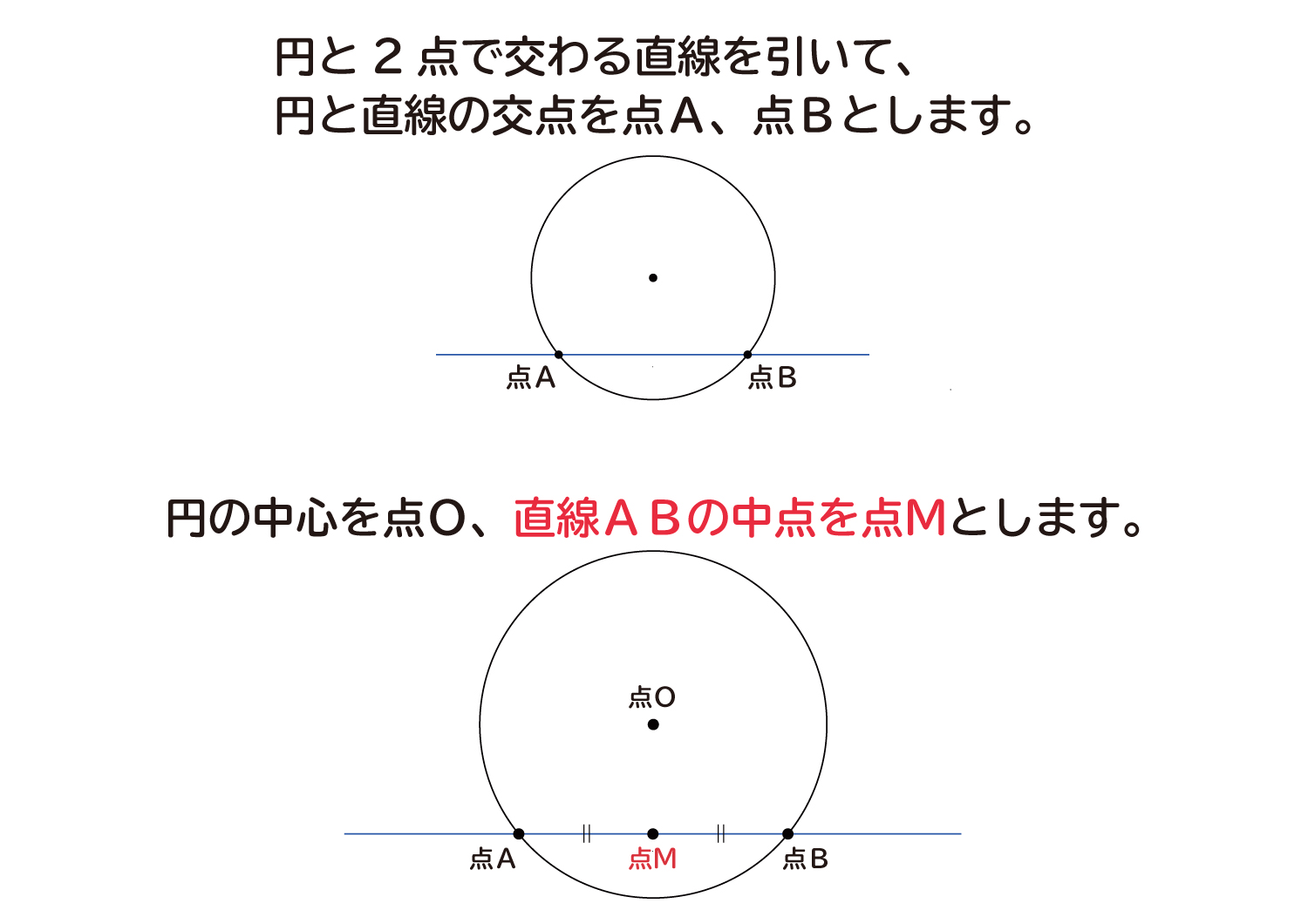
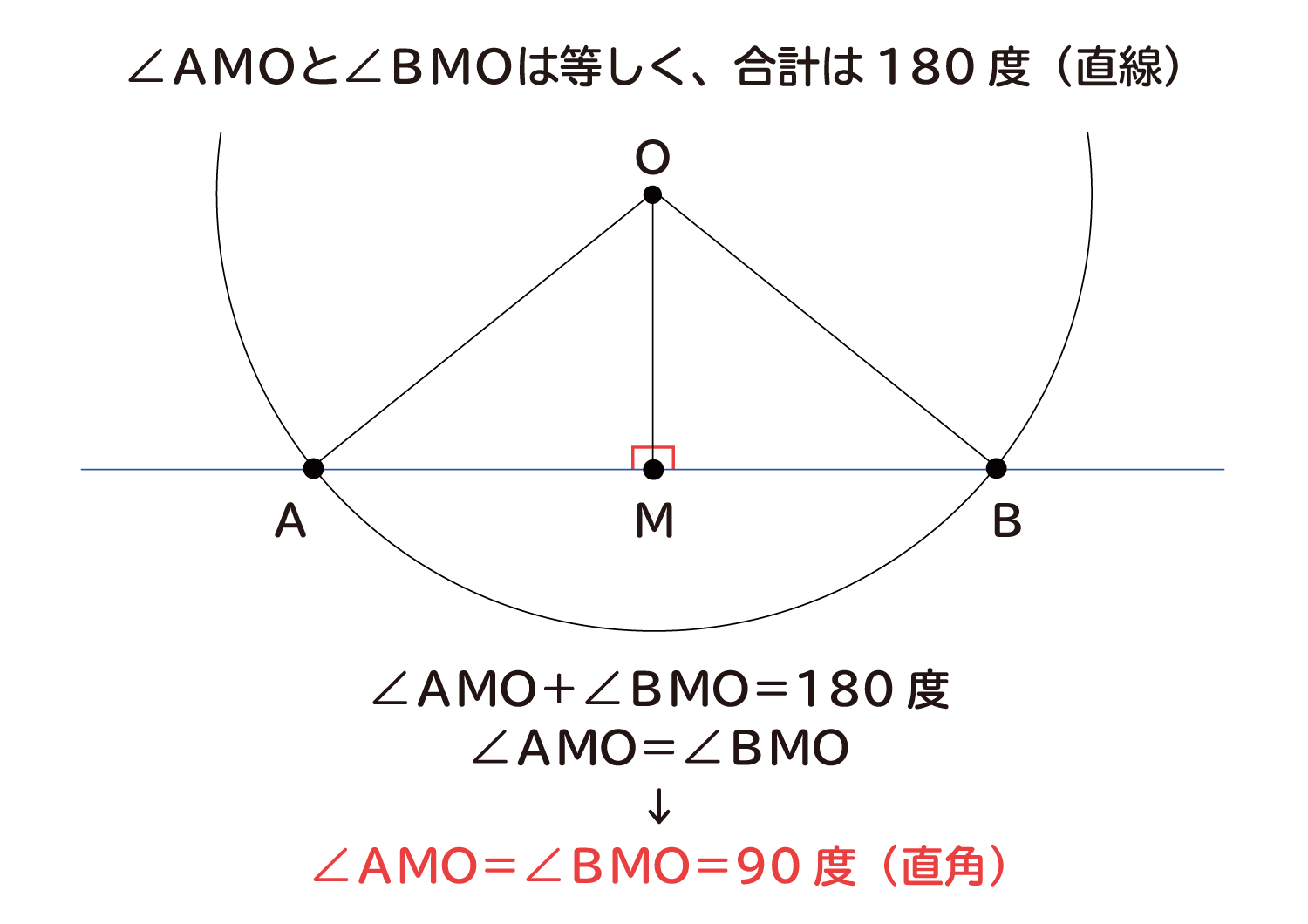
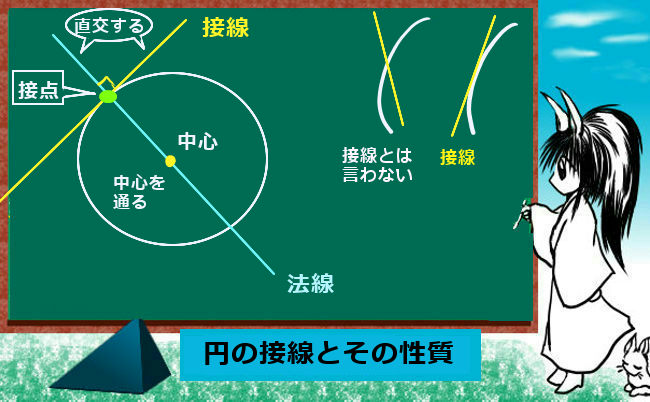
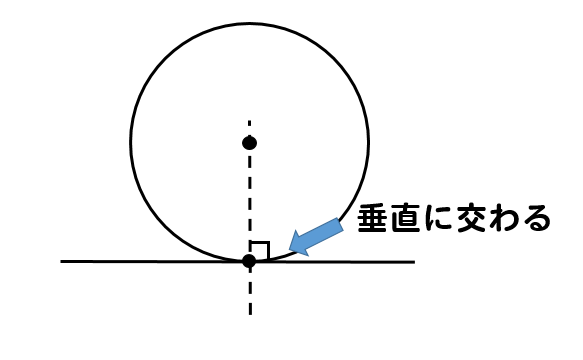
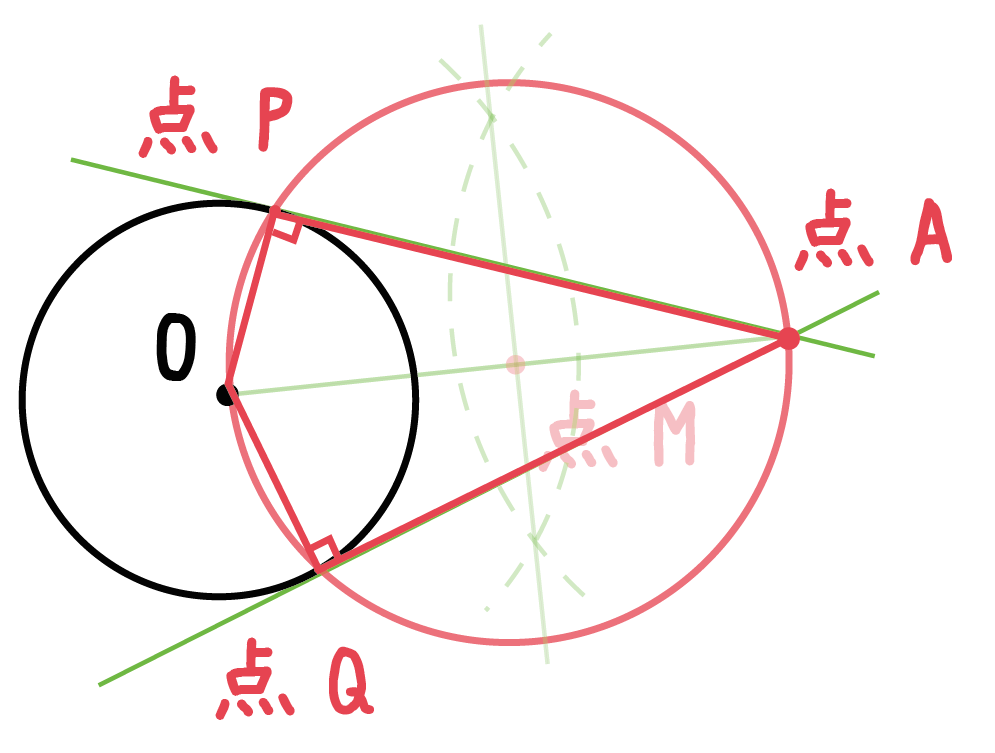
垂直な成分は素通りする。 光は、偏光軸が互いに 垂直な2枚の偏光板を 通過できない。 直線偏光 偏光板:異方性のある結晶。またポリビニルアルコール という高分子材を特定の方向に伸ばすと、細かいシマ 模様の並ぶ偏光板が作れる。「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように円と2点で交わる直線を引いて、円と直線の交点を点A、点Bとします。 円の中心を点O、 直線ABの中点を点M とします。 ここで、三角形AMOと三角形BMOは、3辺の長さが全て同じなので、合同な三角形になっています。証明させる。 ・半径と垂直であれば接線となることを確認する。 ・合同な図形に注目させる。 2a以外にも作図法があることを紹介し,円周角 の定理を利用した作図法を考えさせる。 sができた生徒には,さらに発展させ,2つの 円の共通接線の作図法を考え
なんで 円の接線と 接点を通る円の直径って垂直に交わるんでした Yahoo 知恵袋
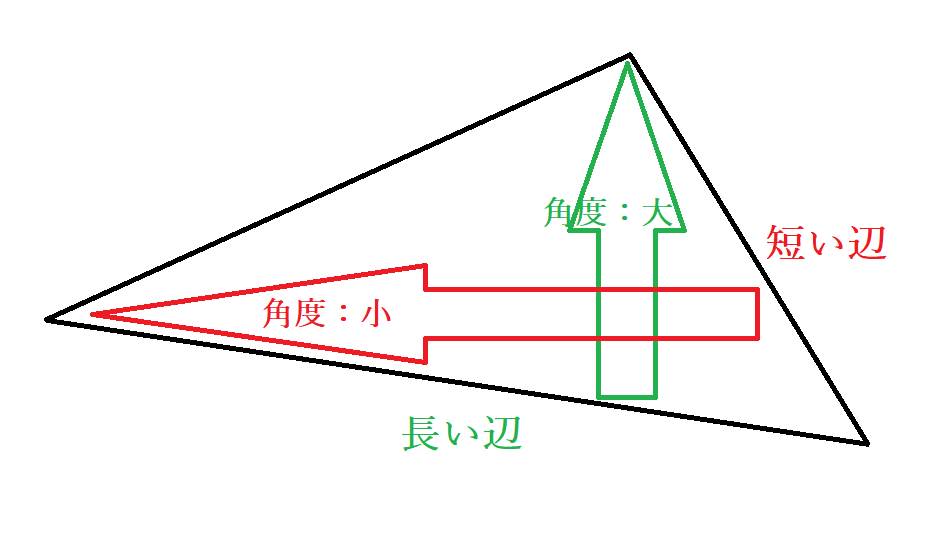
円の接線 垂直 証明
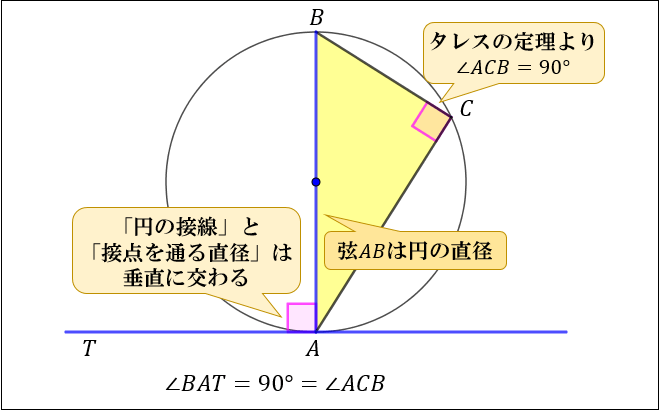
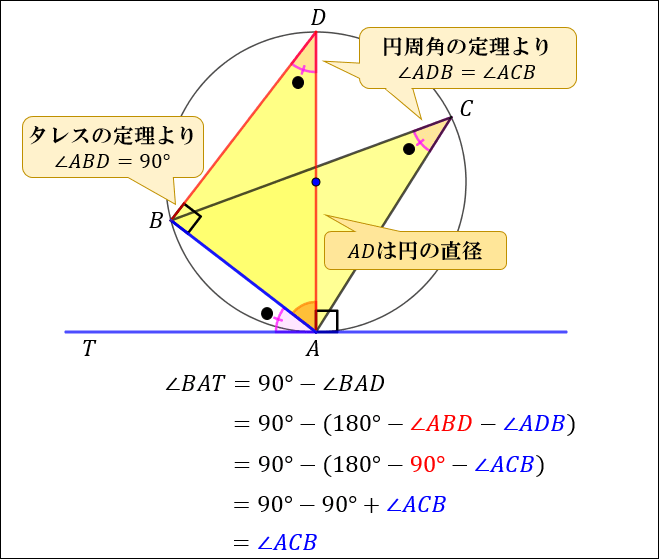
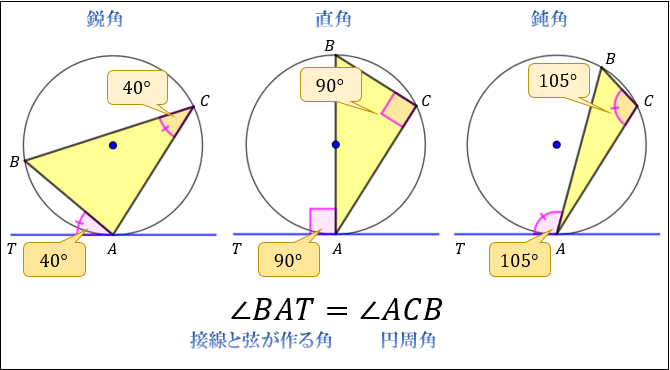
円の接線 垂直 証明-補助円の中心である原点と直線との距離は円の半径に等しいから、 ∴ より公式を得る。 ②の証明) 補助円 x 2 y 2 = 倍すると、 接弦定理とは何か。 角度別に分かるその証明方法 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。 接弦定理は、 ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
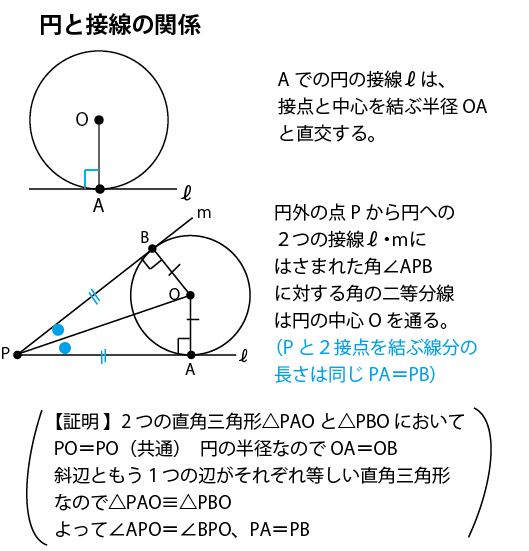
証明しましょう。 この円の中心は原点Oです。 まず点Aが、x軸・y軸上の点ではないとき、 直線OAの傾きは、y1/x1 となります。 また、接線は、円の半径である線分OAと垂直ですから、接線の傾きは、 -x1/y1 となります。②接線と半径は接点で垂直に交わる! ③2本の接線が作る角の二等分線は中心を通る! ④ある線分を直径とする円をかくと円周上に直角ができる! <作図問題> 1 以下の図は,ある円の一部です。ことを証明しなさい。 (p1) 3 次の定理を空らんをうめ確認しなさい。 円外の1点からの接線 定理 円外の1点から,その円にひいた 等 しい。 4 次の図のように,ABを直径とする半 円と,その周上の点Pを通る接線があり ます。
点 (3 , 4) から円 x 2 y 2 =4 にひいた2つの接線の接点を結ぶ直線の方程式を求めよ. x y=4 (2) 点 (4 , 3) から楕円 =1 にひいた2つの接線の接点を結ぶ直線の方程式を求めよ. x y=12 採点する やり等速円運動 : 位置 (pisition) ,速度 (velocity) ,加速度 (acceleration) 原点 O を中心とした半径 r r の円周上を角速度 ω ω で等速円運動する質点の位置 r= (x, y) r = ( x , y) の各成分は と表される( θ0 θ 0 :初期位相).質点の 速度 v =dr/dt v = d r / d t = (vx, vy) = ( v x証明 焦点f2から点p の方向へ、楕円の長軸の長さだけ離れた点をq とする。f1 q の垂直2 等分 線が点p での接線でもある事が次のように示せる。まず、 pf2 pf1 =(長軸の長さ)=f2 q= pf2 pq なのでpf1 =pq であるから、f1 q の垂直2 等分線は点p を通る。
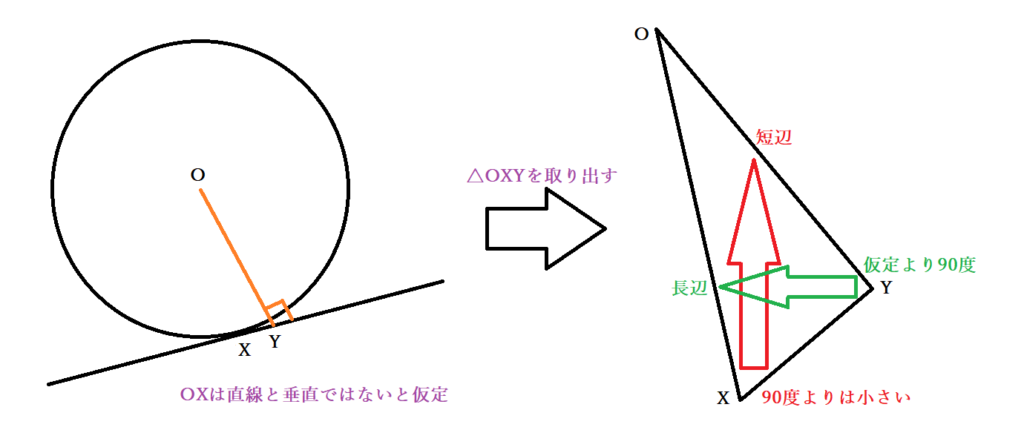
垂直な直線の方程式の求め方と応用 レベル ★ 基礎 座標,ベクトル 更新日時 垂直条件1(傾きの積が−1) 垂直条件2(一般形) 通る一点が指定されるときについて 応用例:楕円の法線の方程式の導出 の順に解説します! 円の接線の方程式を求める公式の3通りの証明 レベル ★ 入試対策 座標,ベクトル 更新日時 座標平面において,円: x 2 y 2 = r 2 x^2y^2=r^2 x2 y2 = r2 上の点円に接し、 中心から接点に 線分が結ばれるならば、 結ばれた線分は 接線に垂直であろう。 これが証明すべきことであった。 本質的に 命題3ー6の補足2(中心は接線の接点での垂線上) で 証明したところである。 接線と円の共有点は接点のみである。



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



Http Www4 Airnet Ne Jp Tmt Mathself Figures8 Pdf
同心円でない2円O,O'がある.2円O,O'に関するべきの等しい点Pの軌跡は2円の中心を結ぶ直線に垂直な 直線である. 証明1 座標を用いた方が分かりやすい. O(0,0),O'(a,b)とおき,円O,O'の半径をそれぞれR,R'とする.接弦定理 円Oの弦ABとその端点Aの接線ATがあるとする。 このとき、 がつくる円周角 は と等しくなる。 これを 接弦定理 と呼ぶ。 1 の場合 以下のように、円の中心Oを通る三角形 を考えます。 となります。 また、 は直角三角形なので 円の接線の式の証明 上の公式の (1) の場合を証明してみましょう.(2) の公式は (1) の場合を平行移動すれば示すことができます. $3$ つの場合に分けて示します.



円の接線の方程式




数 円の基本 円の方程式 円の接線 を完全マスター 公式と証明を丁寧に解説します 高校生向け受験応援メディア 受験のミカタ
円の接線は接点を通る半径に垂直である。 証明 円oの直径abをとる。点bを通る接線と、点aと円周上の点cを結んで延長した線の交点をdとする。 abdと bcdにおいて、 円の接線とその接点を通る弦の作る角は、その角の内部にある孤に対する円周角に等しい このように 「円の中心と接点を結んだ線分」 と 「接線」 は 必ず垂直 になります。これは幾何学の範囲で学んだことです。 ということは、このように考えるのはいかがでしょうか。 接線の方程式は、円の中心と接点を通る直線と垂直に交わる と。 円の接線は、中心と接点を結んだ線と垂直に交わる という知識を知っていないといけません。 これまたよく出題されるので覚えておきましょう。 垂線の作図まとめ! 最後に垂線の作図についてまとめておきましょう。




基本 円の接線の作図 なかけんの数学ノート



円の接線と内接 外接 理数系無料オンライン学習 Kori
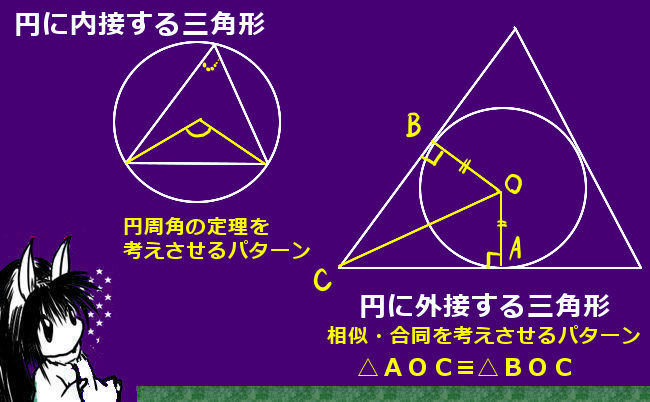
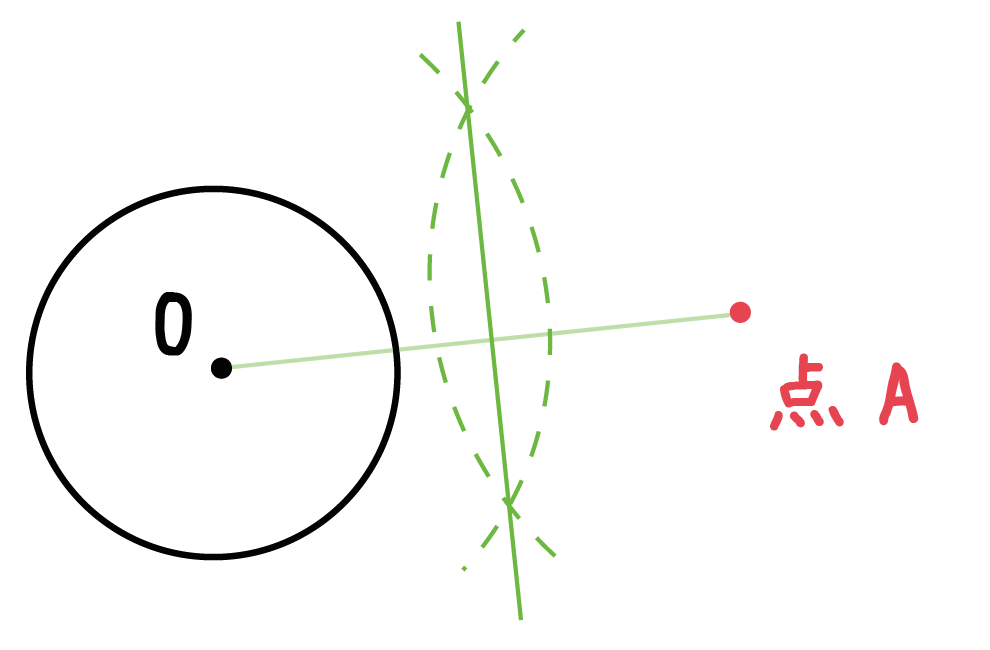
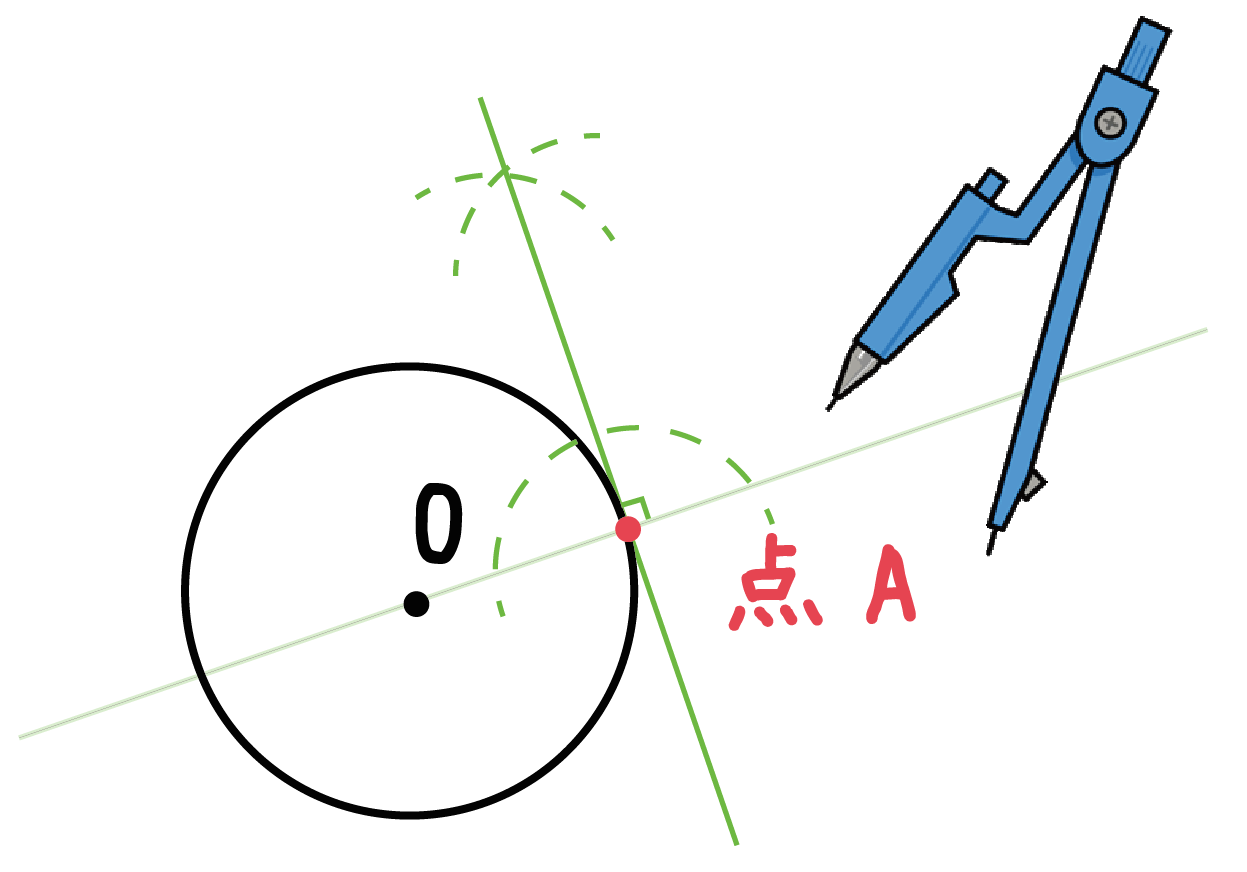
円の中心と接点とを結んだ線分は、接線と垂直となります。 ということは、点 O から、直線 $\ell$ に垂線をおろせば、交点が接点となります。 基本垂線の作図(直線上にない点を通る)その2 で見た内容などを使えば、垂線を作図することができるので円に接す線を 接線 、接する点を 接点 といいます。 POINT:接線は、接点を通る半径に垂直 図の $\rm AO$ を結ぶと $2$ つのことがわかります。 「 円周角の定理の逆 」から POINT: $\textcolor{blue}{2}$ つの接点は、 $\textcolor{blue}{\rm AO}$ を直径とする円周上にある。 直角三角形の合同条件「 斜辺と他2つの円の共通接線 今回は 2 つの円に共通する接線( 共通接線 )を考えてみます。 どんな風に接線が引けるかは,もちろん円と円の位置関係によって変わります。 円と円の位置関係については,前回学びました。 「離れている」「外接する」「 2 点で



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




ねこ騙し数学
傍接円、傍心について 中学生へ 三角形の外角の二等分線の交点を「傍心ほ(ぼ)うしん」といい、傍心は全部で3つあり、下の図で ABCの傍心は点P、Q、R の3つです。 1990年ごろの中学の教科書にも傍心という用語は出てきませんが、傍接円と接線の長さ 双曲線の準円(直交する2本の接線の交点の軌跡) 2直線の平行条件・垂直条件・一致条件とその証明 高校生・受験生への挑戦状!積分最難問ランダム13題(1) 円 上の点 における接線は、 という公式をすぐに 用いて答のみでいいでしょう。 求める接線は、 (2) 図を書いてみると、接線が 2 本存在することが分かりますね。 そのうちの 1 本は、 点 を通り 軸に平行ですから、直線 と分かります。




接弦定理の証明 円周角が直角ver 数学a By となりがトトロ マナペディア




円の接線が半径に垂直であることの証明 Youtube
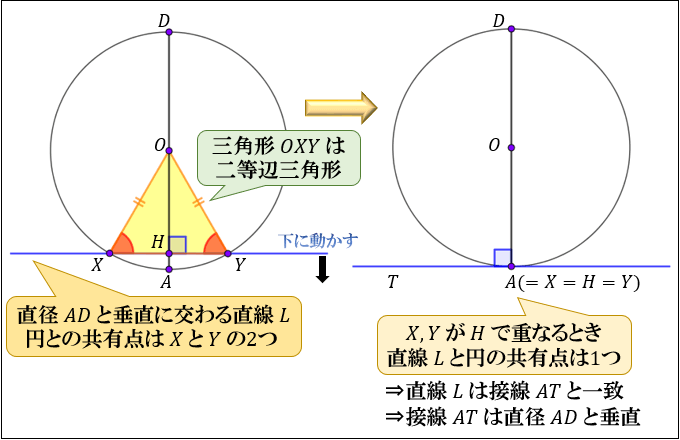
このように、垂直二等分線の作図を利用して 円の接線を作図していきます。 詳しくはこちらの記事で解説しています。 ⇒ 円の接線作図基本作図から2つの円の共通接線まで解説! まとめ 垂直二等分線については以上! まずは書き方の手順を覚えるAをHにもっていくと、BCは円の直径となる。 よって角度は90°となり、Hの放物線への接線は直角ということがわかる。 準線上の放物線への接線は直角なので、Hは準線上にあることがわかる。 証明できた! Geoで証明するコツ円の接線に関する2つの性質「円の接線は接点を通る 半径に垂直である」,「円外の1点から, その円にひいた 2つの接線の長さは等しい」を,極と極線に着目して 見直すと,統合的にみることが可能に



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



48s96ub7b0z5f Net En Sessenn




標準 円の接線と作図 なかけんの数学ノート




円の接線の方程式を求める公式と証明 高校数学の知識庫




Images Of 垂直接線 Japaneseclass Jp



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




接弦定理まとめ 証明 逆の証明 理系ラボ



1
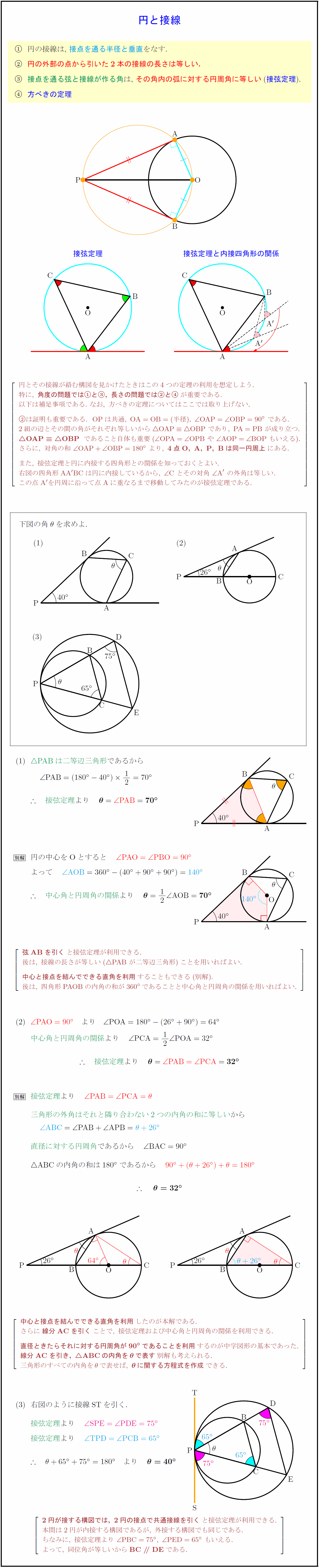



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月




ベクトル方程式 5 怜悧玲瓏 高校数学を天空から俯瞰する




平面図形25 円の接線 怜悧玲瓏 高校数学を天空から俯瞰する



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
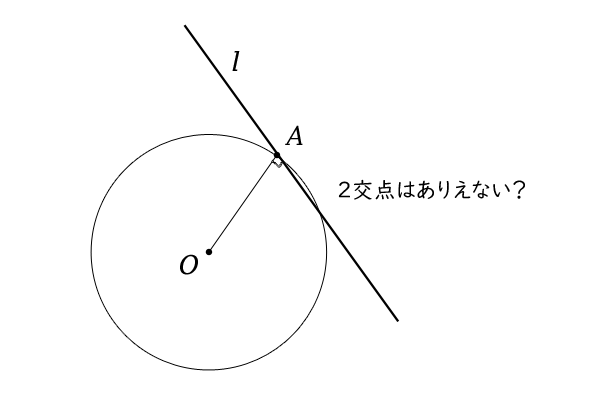



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




円の接線の長さの証明 数学a By となりがトトロ マナペディア




円の接線 その基本的な性質 番外編 身勝手な主張



円の接線




高校数学a 接線と接線の長さ 練習編 映像授業のtry It トライイット




平面図形 4 円 円と直線 伊東市の家庭教師
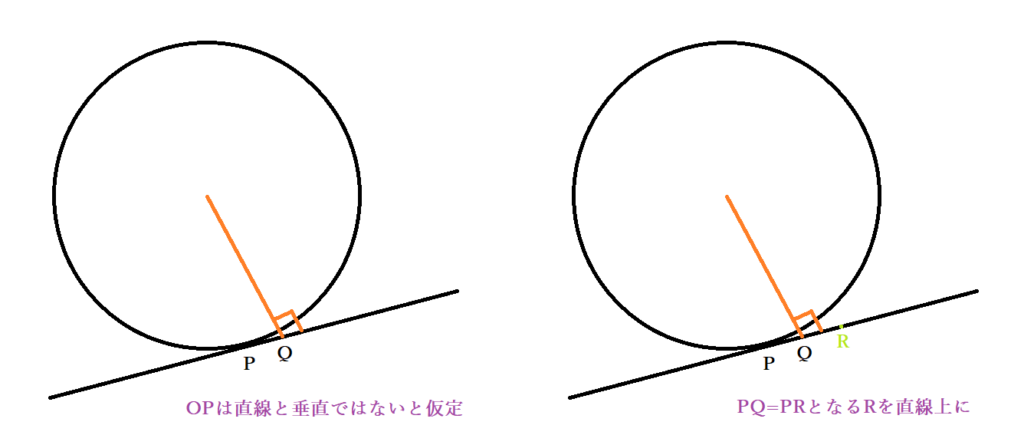



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
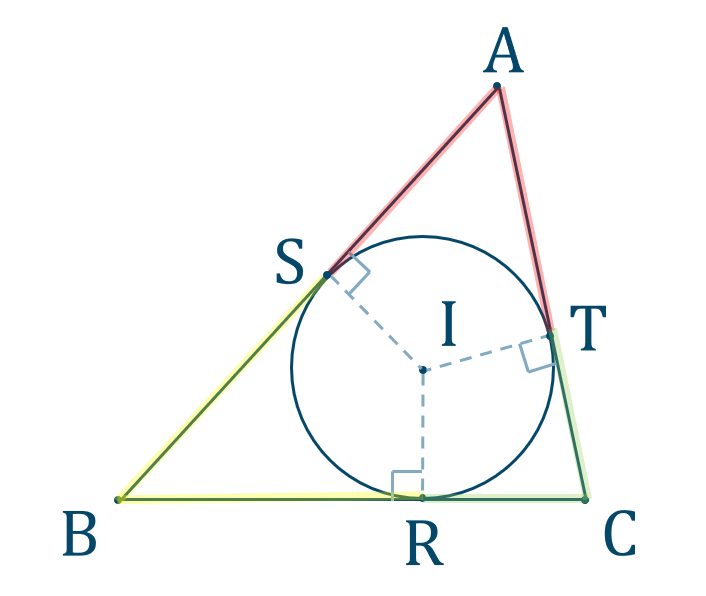



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



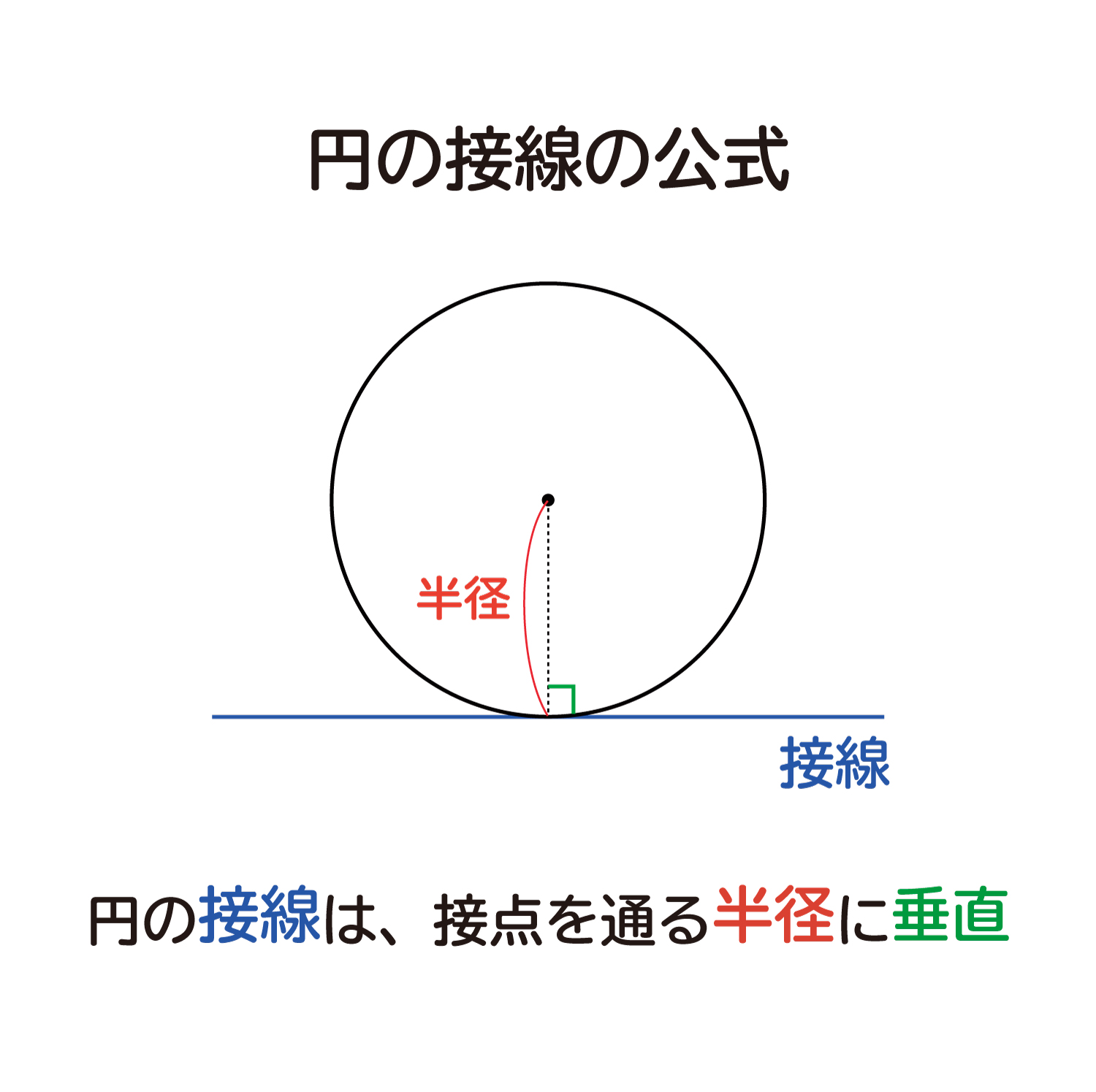
なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




円の接線の方程式の導出方法 数学の偏差値を上げて合格を目指す



2円の共通外接線の作図 懐かしの家族hp 楽天ブログ




高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月




円の接線の方程式を求める公式と証明 高校数学の知識庫



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
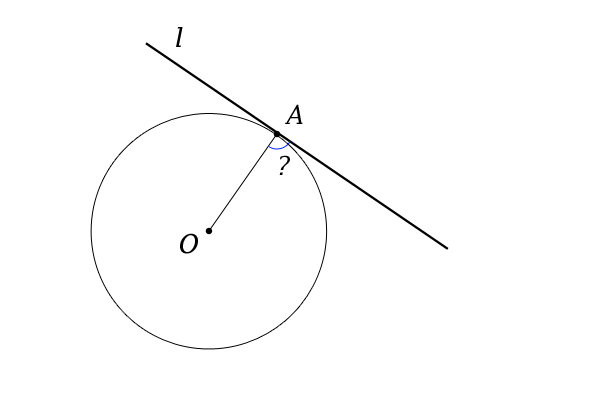



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター



数学a 平面図形 円の性質 円の接線



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




図形の性質がわかません 図の Oebが90度になる理由がわかりません Okwave




うさぎめし C 証明



数学の質問です 円の接線は 中心と接点を結ぶ線分 半径 と垂直 Yahoo 知恵袋



1
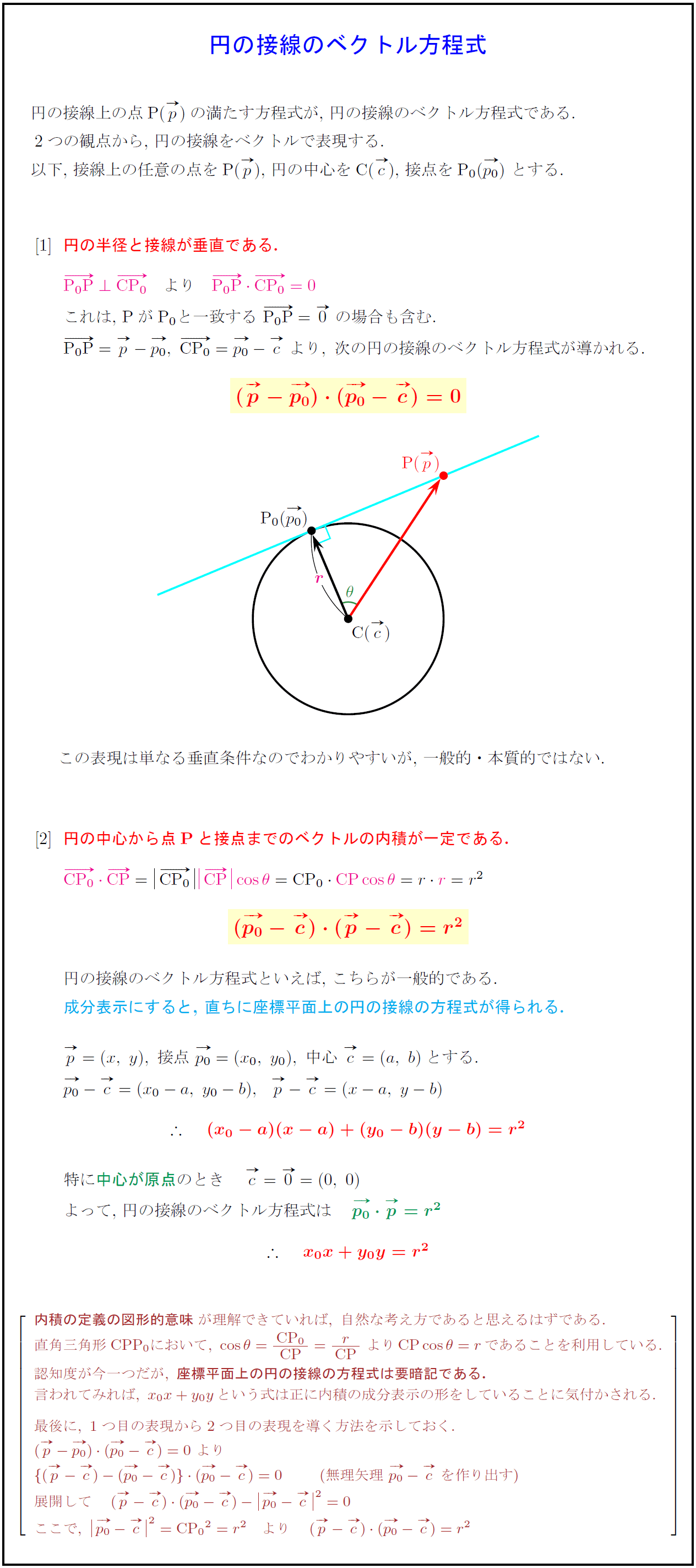



高校数学b 円の接線のベクトル方程式2パターン 受験の月




円の接線の方程式とその証明 おいしい数学




円の接線の方程式とその証明 おいしい数学




接線と円の関係 Jsciencer



中学数学について質問します 何故円の接線に垂直な線は円の中心を通るのです Yahoo 知恵袋




高校数学 円外の点から引いた接線の方程式 受験の月



円と直線の関係
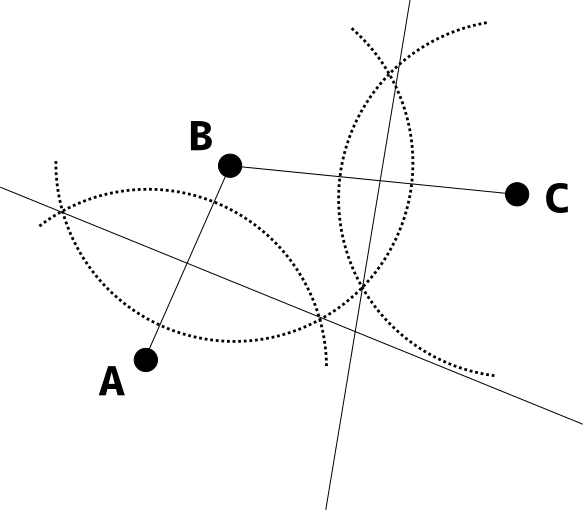



円の作図と円の接線の作図 チーム エン



円の接線の求め方 思考力を鍛える数学



なんで 円の接線と 接点を通る円の直径って垂直に交わるんでした Yahoo 知恵袋
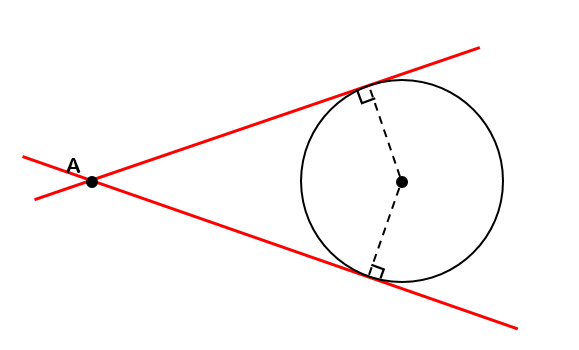



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
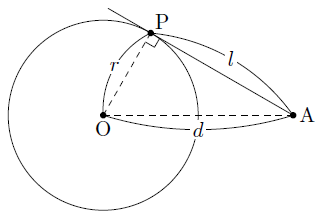



円の接線の長さ まなびの学園




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




第3巻命題18 接線と半径は垂直 Stoixeia ストイケイア




数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




基本 垂線の作図 直線上にない点を通る その2 なかけんの数学ノート




証明 円の接線は接点を通る半径に垂直である



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




連質本当に本当にsorryでございます 1枚目 1 合ってますか Clear




円の接線に関する定理 公式 数a範囲 数学の偏差値を上げて合格を目指す



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




中学数学 円と接線 Youtube



円の接線の方程式証明について この問題解説の赤枠で囲ってい Yahoo 知恵袋




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



3




数学ii 図形と方程式 6 4 円上の点における接線の方程式 Youtube
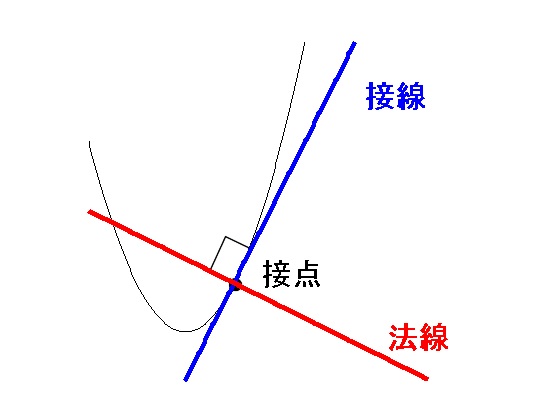



微分を使った接線に垂直な法線の方程式の求め方と公式
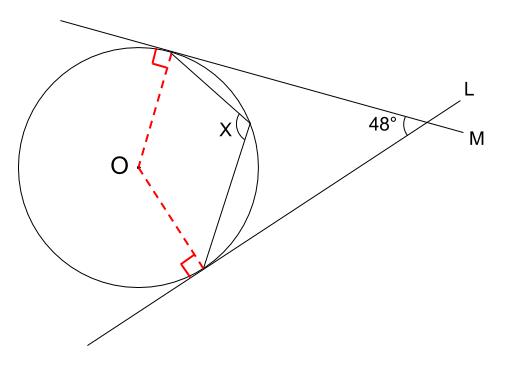



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円の接線の求め方 思考力を鍛える数学



円の接線と内接 外接 理数系無料オンライン学習 Kori




第3巻命題18 接線と半径は垂直 Stoixeia ストイケイア



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog



円の接線の方程式




円の接線の方程式 数学 の授業から 身勝手な主張




Emath 高校数学 円の接線 円の外部から の攻略 数樂管理人のブログ
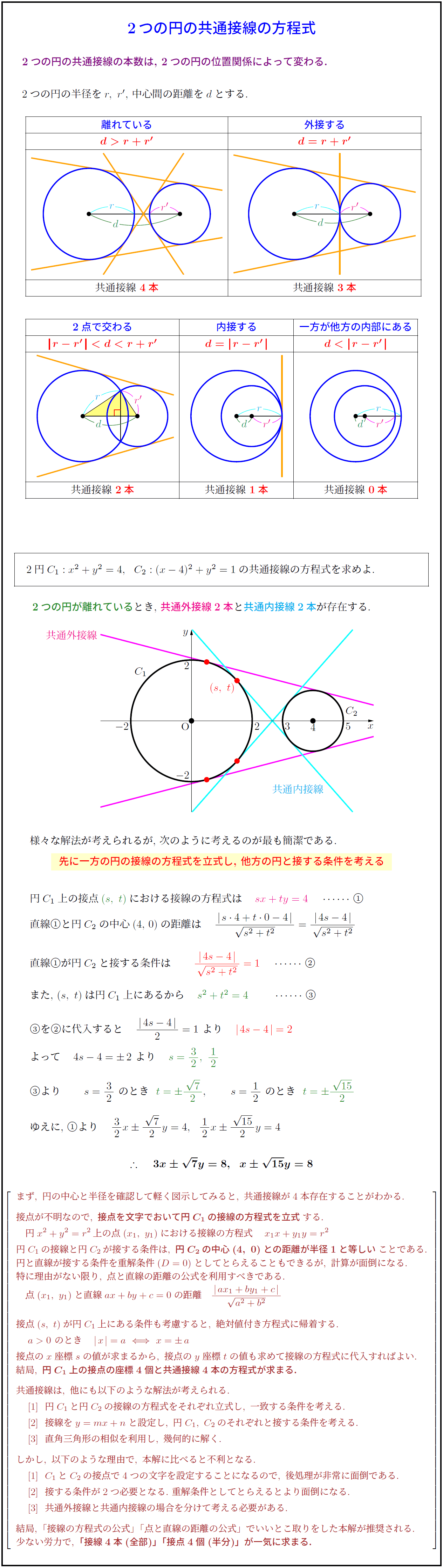



高校数学 2つの円の共通接線の方程式 受験の月




放物線の接線になる条件 Geogebra




数学の世界をのぞいてみよう 第42回 円の接線と弦のなす角は弦をふくむ円周角と等しい Segブログ 科学的教育グループseg
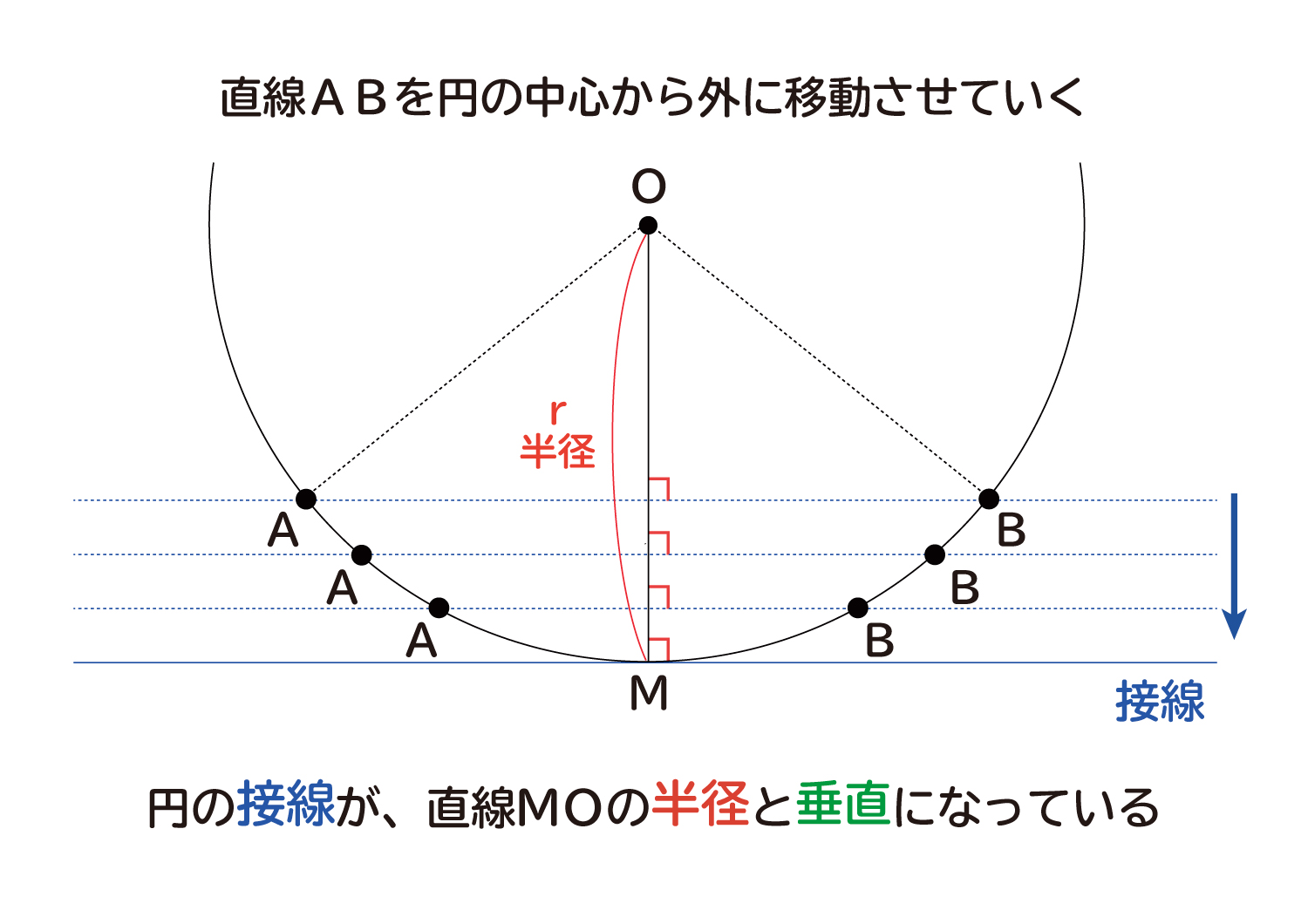



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




証明の2行目 円の接線の性質からqa Qp Qb とありますが 何故ですか Clear




Emath 高校数学 円の接線 円の外部から の攻略 数樂管理人のブログ



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ



17年前期 千葉県公立高校入試数学 第2問 5 作図 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



証明 円の接線は接点を通る半径に垂直である



円の接線は 接点を通る半径に垂直なのはなぜですか 教えてください よろし Yahoo 知恵袋



中学数学 円周角 中心角




円の接線が直径と垂直に交わることの証明 うさぎめし C



働きアリ February 02 12




知ってると得 円の接線の作図 円に接する円の作図方法 はてなラボ



証明 円の接線は接点を通る半径に垂直である




接弦定理の証明 円周角が直角ver 数学a By となりがトトロ マナペディア




接弦定理まとめ 証明 逆の証明 理系ラボ



3



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく
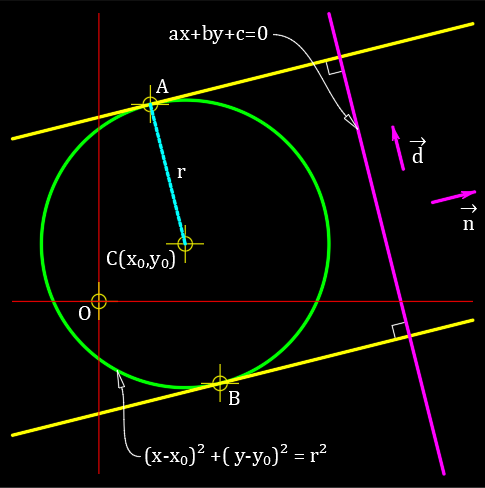



直線に垂直な円の接線の方程式を求める Qiita




高校数学 2円の外接 共通接線 図のように 2円が外接していて 共通接線 Okwave




高校数学 円周上の点における接線の方程式 X X Y Y R とその証明 受験の月
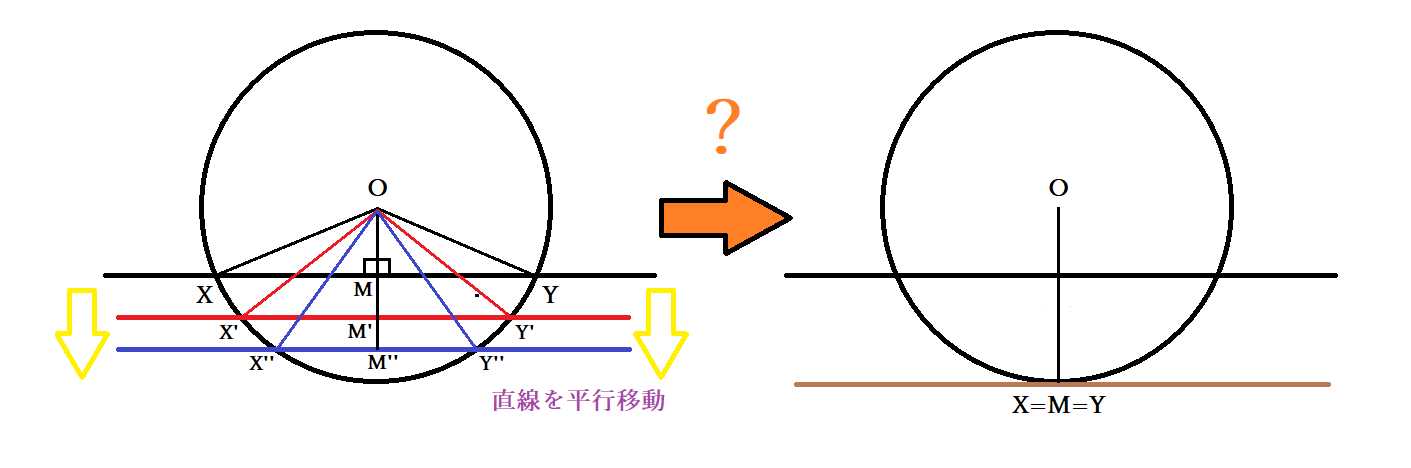



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




高校数学a 共通接線の長さを求める問題 例題編 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿